
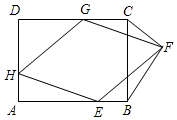
 已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.
已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.分析 (1)由于四边形ABCD为矩形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;
(2)欲求△EBF的面积,由已知得BE的长,只需求出BE边的高,通过证明△HDG≌△FME可得;易证△HAE≌△FNG,用x表示出△CGF的面积,根据题意列方程即可.
解答 (1)证明:在△HDG和△AEH中,
∵四边形ABCD是矩形,
∴∠D=∠A=90°
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HDG和Rt△AEH中,
$\left\{\begin{array}{l}{HG=HE}\\{DG=AH}\end{array}\right.$,
∴Rt△HDG≌Rt△AEH,
∴∠DHG=∠AEH,
∴∠DHG+∠AHE=90°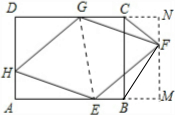
∴∠GHE=90°,
∴菱形EFGH为正方形;
(2)解:过F作FM⊥AB,垂足为M,交DC延长线于点N,连接GE,
∴FN⊥CD,
∵CD∥AB,
∴∠DGE=∠MEG,
∵GH∥EF,
∴∠HGE=∠FEG,
∴∠DGH=∠MEF,
在Rt△HDG和Rt△FME中,
$\left\{\begin{array}{l}{∠D=∠M=90°}\\{∠DGH=∠FEM}\\{HG=FE}\end{array}\right.$,
∴Rt△HDG≌Rt△FME,
∴DH=MF,
∴AH=2,
∴DH=MF=4,
∵AE=x,
∴BE=10-x.
∴S△EBF=$\frac{1}{2}$BE•FM=2(10-x)=20-2x.
同理可证Rt△AHE≌Rt△FNG,
∴FN=AH=2,
∵AH=2,AE=x,
∴HE=HG=$\sqrt{A{H}^{2}+A{E}^{2}}$=$\sqrt{{x}^{2}+4}$,
∴DG=$\sqrt{H{G}^{2}-D{H}^{2}}$=$\sqrt{{x}^{2}+4-16}$=$\sqrt{{x}^{2}-12}$,
∴CG=10-$\sqrt{{x}^{2}-12}$,
∴S△GCF=$\frac{1}{2}$CG•FN=10-$\sqrt{{x}^{2}-12}$,
若△EBF的面积是△CGF面积2倍,则
20-2x=2(10-$\sqrt{{x}^{2}-12}$)
整理得:x2=x2-12,
此方程无解,
所以不存在x,使△EBF的面积是△CGF面积2倍.
点评 本题考查了矩形的性质、菱形的性质、全等三角形的判定和性质,解题的关键是作辅助线:过F作FM⊥AB,交AB延长线于M,交DC延长线于点N,连接GE,构造全等三角形和内错角.


科目:初中数学 来源: 题型:解答题
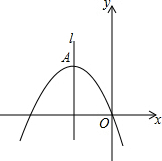 如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
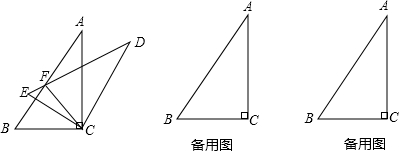
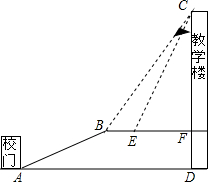 重庆是一座美丽的山城,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在斜坡B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米
重庆是一座美丽的山城,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在斜坡B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com