
分析 根据增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x-1)(x+2)=0,得到x=1或-2,然后代入化为整式方程的方程算出a的值.
解答 解:方程的两边都乘以(x-1)(x+2),得
3(x+2)-(x-1)=m,化简,得
2x+3=m.
∵原方程有增根,
∴最简公分母(x-1)(x+2)=0,
解得x=1或-2,
当x=1时m=5,
当x=-2时,m=2×(-2)+3=-1,
故答案为:-1或5.
点评 本题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:填空题
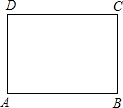 如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)
如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
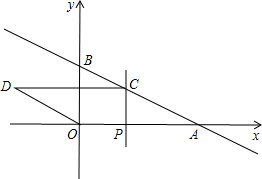 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P为x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA、AC为边构造平行四边形OACD,设点P的横坐标为m.
如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P为x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA、AC为边构造平行四边形OACD,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
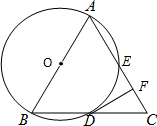 如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.
如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 5π | B. | $\frac{3π}{2}$ | C. | $\frac{13π}{2}$ | D. | $\frac{23π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com