
如图,在△ABC中,AD为角平分线,CE⊥AD,F为BC中点.
求证:EF= (AB-AC).
(AB-AC).

证明:如图,延长CE交AB于G,
∵AD为角平分线,
∴∠EAG=∠EAC,
∵CE⊥AD,
∴∠AEG=∠AEC=90°,
在△AGE和△ACE中,
∠EAG=∠EAC, AE=AE, ∠AEG=∠AEC=90°,
∴△AGE≌△ACE(ASA),
∴AG=AC,CE=GE,
又∵F为BC中点,
∴EF是△BCG的中位线,
∴EF=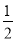 BG=
BG=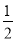 (AB-AG)=
(AB-AG)=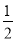 (AB-AC),
(AB-AC),
即EF=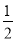 (AB-AC).
(AB-AC).

【解析】
延长CE交AB于G,利用“角边角”证明△AGE和△ACE全等,根据全等三角形对应边相等可得AG=AC,CE=GE,然后求出EF是△BCG的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半证明即可.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:选择题
如图所示,AE是△FCD的中位线,BD∥AC,A,E,B三点共线,AB=8,FA=FE=6,则下列说法:①BE=4;②∠DEB=∠DBE;③AF=BD;④CD=2AE.正确的结论是( )

A.①②④ B.①②③ C.①③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下7.1算术平方根 题型:选择题
一个数的算术平方根只要存在,那么这个算术平方根 ( )
A.只有一个,并且是正数
B.不可能等于零
C.一定小于这个数
D.必定是非负数
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:解答题
如图,在△ABC中,CE平分∠ACB,AE⊥CE,延长AE交BC于点F,D是AB的中点,BC=20,AC=14,求DE的长.

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:填空题
如图,△ABC的三边长分别为3、5、6,BD与CE都是△ABC的外角平分线,M、N是直线BC上两点,且AM⊥BD于D,AN⊥CE于E,则DE的长等于________.

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下7.2勾股定理 题型:选择题
直角三角形的斜边长为10,一直角边长是另一直角边长的3倍,则直角三角形的面积为( )
A.12 B.13 C.14 D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com