
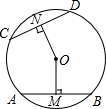
 如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB=CD,求证:OM=ON.
如图,AB和CD分别是⊙O上的两条弦,圆心O到它们的距离分别是OM和ON,如果AB=CD,求证:OM=ON. 分析 连接OA、OC,根据垂径定理求出CD=2CN,AB=2AM,求出CN=AM,根据HL证Rt△ONC≌Rt△OMA,根据全等三角形的性质推出即可.
解答 证明:如图,连接OC、OA,则OC=OA,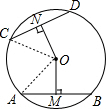
∵圆心O到它们的距离分别是OM和ON,
∴∠ONC=∠OMA=90°,CD=2CN,AB=2AM,
∵AB=CD,
∴CN=AM,
在Rt△ONC和Rt△OMA中,
$\left\{\begin{array}{l}{OC=OA}\\{CN=AM}\end{array}\right.$,
∴Rt△ONC≌Rt△OMA(HL),
∴OM=ON.
点评 本题考查了垂径定理,全等三角形的性质和判定的应用,解此题的关键是构造直角三角形,题目比较典型,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
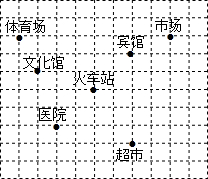 如图,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其它各地点的坐标.
如图,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其它各地点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
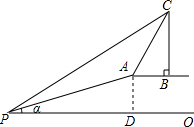 如图,在一斜坡坡顶A处的同一水平线上有一古塔,为测量塔高BC,数学老师带领同学在坡脚P处测得斜坡的坡角为α,且tanα=$\frac{7}{24}$,塔顶C处的仰角为30°,他们沿着斜坡攀行了50米,到达坡顶A处,在A处测得塔顶C的仰角为60°.
如图,在一斜坡坡顶A处的同一水平线上有一古塔,为测量塔高BC,数学老师带领同学在坡脚P处测得斜坡的坡角为α,且tanα=$\frac{7}{24}$,塔顶C处的仰角为30°,他们沿着斜坡攀行了50米,到达坡顶A处,在A处测得塔顶C的仰角为60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形A1B1C1O,A2B2C2B1、A3B3C3B2,…,按如图的方式放置,点A1、A2、A3,…和点C1、C2、C3,…分别在直线y=x+1和x轴上,则点B2015的纵坐标是22014.
正方形A1B1C1O,A2B2C2B1、A3B3C3B2,…,按如图的方式放置,点A1、A2、A3,…和点C1、C2、C3,…分别在直线y=x+1和x轴上,则点B2015的纵坐标是22014.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
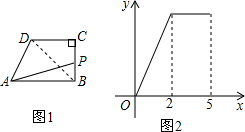 如图(1),在直角梯形ABCD中,AB∥CD,∠ABC=90°,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则△BCD的面积是( )
如图(1),在直角梯形ABCD中,AB∥CD,∠ABC=90°,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则△BCD的面积是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com