Question

【题目】

（1）解题探究

已知三角形ABC,探究∠A+∠B+∠C等于多少度？（提示：过一点作平行线）

（2）发现规律

如图①，三角形ABC中，点D在BC的延长线上，试说明∠A+∠B与∠1的关系？

（3）运用规律

利用以上规律，快速探究以下各图：

当AB∥CD时，∠A，∠C，∠P的关系式为（直接填空，不要证明过程）：

∠C = ，∠C = ，∠C =

Answer 1

【答案】(1)180°；（2）∠A+∠B=∠1；（3）∠A+∠P，∠A-∠P，∠P+180°-∠A.

【解析】试题分析：（1）延长BC到D，过点C作CE∥BA，根据两直线平行，同位角相等可得∠B=∠1，两直线平行，内错角相等可得∠A=∠2，再根据平角的定义列式整理即可得证；

（2）根据平行线的性质即可得到结论；

（3）根据平行线的性质和三角形的外角的性质即可得到结论．

试题解析：（1）如图⑤，延长BC到D，过点C作CE∥BA，

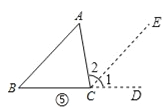
∵BA∥CE，

∴∠B=∠1（两直线平行，同位角相等），

∠A=∠2（两直线平行，内错角相等），

又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），

∴∠A+∠B+∠ACB=180°（等量代换）；

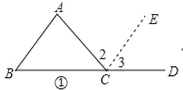
（2）如图①过C作CE∥AB，

∴∠2=∠A，∠3=∠B，

∴∠ACD=∠1+∠2=∠A+∠B，

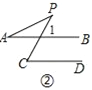
（3）如图②，∵AB∥CD，

∴∠1=∠C，

∵∠1=∠A+∠P，

∴∠C=∠A+∠P；

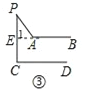
如图③，延长BA交PC于E，

∵AB∥CD，

∴∠1=∠C，

∴∠1=∠C=∠BAP﹣∠P；

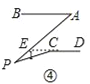
如图④，

延长CD交AP于E，

∵AB∥CD，

∴∠A=∠AEC=∠P+，

∴∠PCD=∠P+180°﹣∠A．

故答案为：∠A+∠P，∠BAP﹣∠P，∠P+180°﹣∠A．