
分析 (1)方程有两个实数根,必须满足△=b2-4ac≥0,从而建立关于m的不等式,求出实数m的取值范围.
(2)找出符合条件的m的最小整数,然后解一元二次方程即可.
解答 解:(1)由题意知:△=b2-4ac=[-2(m+1)]2-4m2=[-2(m+1)+2m][-2(m+1)-2m]=-2(-4m-2)=8m+4≥0,
解得m≥-$\frac{1}{2}$.
∴当m≥-$\frac{1}{2}$时,方程有两个实数根;
(2)取m=0,
方程为x2-2x=0,
解得x1=0,x2=2.
点评 此题考查了一元二次方程的根的判别式,能够根据一元二次方程的根的判别式和方程的根的情况求得字母m的取值范围,此题难度一般.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
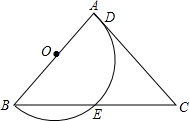 如图,△ABC中,AB=AC,∠A=80°,以AB为直径的半圆交AC于D,交BC于E,求$\widehat{AD}$、$\widehat{DE}$、$\widehat{BE}$所对圆心角的度数.
如图,△ABC中,AB=AC,∠A=80°,以AB为直径的半圆交AC于D,交BC于E,求$\widehat{AD}$、$\widehat{DE}$、$\widehat{BE}$所对圆心角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com