Question

8．如图，已知双曲线y=$\frac{m}{x}$（m＞0）与直线y=kx交于A、B两点，点A的坐标为（3，2）． 
（1）由题意可得m的值为6，k的值为$\frac{2}{3}$，点B的坐标为（-3，-2）；
（2）若点P（n-2，n+3）在第一象限的双曲线上，试求出n的值及点P的坐标；
（3）在（2）小题的条件下：如果M为x轴上一点，N为y轴上一点，以点P、A、M、N为顶点的四边形是平行四边形，试求出点M的坐标．

Answer 1

分析 （1）把A坐标代入反比例解析式求出m的值，确定出反比例解析式，把A坐标代入直线解析式求出k的值，利用对称性求出B坐标即可；
（2）把P坐标代入反比例解析式求出n的值，确定出P坐标即可；
（3）分两种情况考虑：当M₁在x轴正半轴，N₁在y轴上半轴时，如图1所示；当M₂在x轴负半轴，N₂在y轴下半轴时，如图2所示，分别求出M坐标即可．

解答 解：（1）把A（3，2）代入反比例解析式得：m=6；
把A（3，2）代入直线解析式得：k=$\frac{2}{3}$，
由对称性得：B（-3，-2）；
故答案为：6；$\frac{2}{3}$；（-3，-2）；
（2）把P（n-2，n+3）代入y=$\frac{6}{x}$中得：（n-2）（n+3）=6，
整理得：n²+n-12=0，即（n-3）（n+4）=0，
解得：n=3或n=-4（舍去），
则P（1，6）；
（3）分两种情况考虑：
当M₁在x轴正半轴，N₁在y轴上半轴时，如图1所示，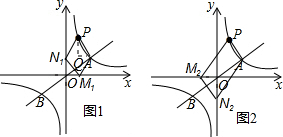

过P作PQ∥y轴，过A作AQ∥x轴，交于点Q，
∵A（3，2），P（1，6），
∴AQ=3-1=2，
由平移及平行四边形性质得到OM₁=2，即M₁（2，0）；
当M₂在x轴负半轴，N₂在y轴下半轴时，如图2所示，
同理得到OM₂=2，即M₂（-2，0）．

点评 此题属于反比例函数综合题，涉及的知识有：待定系数法求反比例函数及一次函数解析式，坐标与图形性质，平移的性质，平行四边形的性质，熟练掌握待定系数法是解本题的关键．