
 如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=$\frac{3}{2}$.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是$\frac{9}{2}$或$\frac{27}{2}$.
如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=$\frac{3}{2}$.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是$\frac{9}{2}$或$\frac{27}{2}$. 分析 设A(2m,3m)、B(2n,3n),当OC=2AD时,能找出点D为线段BC中点,从而得出m、n间的关系,将A、B点坐标代入抛物线与抛物线对称轴x=2m联立方程组,解方程组即可求得c的值.
解答 解:由tan∠AOE=$\frac{3}{2}$,可设A、B点坐标分别为(2m,3m)、(2n,3n),
∵AD∥OC,
∴∠ADB=∠OCB,∠DAB=∠COA,
∴△BAD∽△BOC.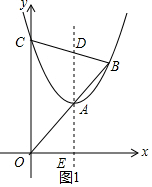
∵OC=2AD,
∴D点为线段BC的中点,
∵C(0,c),B(2n,3n),
∴D点横坐标为$\frac{0+2n}{2}$=n,
由题意知A、D点均在抛物线的对称轴上,
∴n=2m,
∴B点坐标为(4m,6m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有$\left\{\begin{array}{l}{3m=4{m}^{2}+2bm+c}\\{6m=16{m}^{2}+4bm+c}\\{-\frac{b}{2}=2m}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=0}\\{b=0}\\{c=0}\end{array}\right.$,或$\left\{\begin{array}{l}{m=\frac{3}{4}}\\{b=-3}\\{c=\frac{9}{2}}\end{array}\right.$,
∵c>0,
∴c=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了三角形的相似以及二次函数的性质,解题的关键是根据OC=2AD找到A、B点坐标的关系.


科目:初中数学 来源: 题型:选择题
| A. | x=$-\frac{1}{2}$,y为任意实数 | B. | x为任意实数,y=$\frac{2}{3}$ | ||
| C. | x=$-\frac{1}{2}$,y=$\frac{2}{3}$ | D. | x为任意实数,y=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知双曲线y=$\frac{m}{x}$(m>0)与直线y=kx交于A、B两点,点A的坐标为(3,2).
如图,已知双曲线y=$\frac{m}{x}$(m>0)与直线y=kx交于A、B两点,点A的坐标为(3,2). 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某窗户由矩形和弓形组成,已知弓形的跨度AB=6m,弓形的高EF=2m,现设计安装玻璃,请帮工程师求出$\widehat{AB}$所在圆O的半径.
如图,某窗户由矩形和弓形组成,已知弓形的跨度AB=6m,弓形的高EF=2m,现设计安装玻璃,请帮工程师求出$\widehat{AB}$所在圆O的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )| A. | 大于60° | B. | 小于60° | C. | 大于45° | D. | 小于45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com