
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
① 当x取什么值时,y>0 ?
② 当x取什么值时,y的值随x的增大而减小?
(1)抛物线的解析式为y=-x2+2x+3;(2)抛物线与x轴的交点坐标(-1,0),(3,0);(3)详见解析;(4)①当-1<x<3时,y>0;②当x>1时,y的值随x的增大而减小.
【解析】
试题分析:(1)将(0,3)代入y=-x2+(m-1)x+m求得m,即可得出抛物线的解析式;
(2)令y=0,求得与x轴的交点坐标;令x=0,求得与y轴的交点坐标;
(3)得出对称轴,顶点坐标,画出图象即可;
(4)当y>0时,即图象在一、二象限内的部分;当y<0时,即图象在一、二象限内的部分;在对称轴的右侧,y的值随x的增大而减小.
试题解析:(1)∵抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点,
∴m=3,
∴抛物线的解析式为y=-x2+2x+3;
(2)令y=0,得x2-2x-3=0,
解得x=-1或3,
∴抛物线与x轴的交点坐标(-1,0),(3,0);
令x=0,得y=3,
∴抛物线与y轴的交点坐标(0,3);
(3)对称轴为x=1,顶点坐标(1,4),图象如图,

(4)如图,①当-1<x<3时,y>0;
当x<-1或x>3时,y<0;
②当x>1时,y的值随x的增大而减小.
考点:1.抛物线与x轴的交点;2.二次函数的图象;3.待定系数法求二次函数解析式.


科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校八年级上学期期中数学试卷(解析版) 题型:填空题
如图,以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积 = .
= .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:选择题
已知△ABC≌△DEF,且AB=DE,AB=2,AC=4,△DEF的周长为偶数,则EF的长为( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,∠AOB=30O,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是( )

A.10 B.15 C.20 D.25
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:解答题
(14分)如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE。

(1)若要使△ACD≌△EBD,应添上条件:__________
(2)证明上题:
(3)在△ABC中,若AB=5.AC=3,可以求得BC边上的中线AD的取值范围AD<4.请看解题过程:
由△ACD≌△EBD得:AD=ED,BE=AC=3,因此AE<AB+BE,即AE<8,而AD= AE,
AE,
则AD<4,请参考上述解题方法,可求得AD>m,则m的值为_______________.
(4)证明:直角三角形斜边上的中线等于斜边的一半。(提示:画出图形,写出已知,求证,并加以证明)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC,点O在△ABC内,且 ∠OBC=∠OCA,∠BOC=110°,求∠A的度数=_______________

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市塘下学区七年级上学期期中联考数学试卷(解析版) 题型:填空题
(6分)把下列各数填在相应的横线上
-5,π, ,
, ,
,
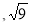 , -0.2,1.6,
, -0.2,1.6, , 0, 1.1010010001……(每两个1之间多一个0)
, 0, 1.1010010001……(每两个1之间多一个0)
整数______________________________________.
负分数______________________________________
无理数______________________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com