Question

【题目】如图，OABC的顶点A的坐标为（3，0），∠COA=60°，D为边AB的中点，反比例函数y=（k＞0）的图象经过C、D两点，直线CD交y轴于点E，则OE的长为 ．

Answer 1

【答案】3

【解析】

试题分析：作CE⊥x轴于点E，过B作BF⊥x轴于F，过D作DM⊥x轴于M，设C的坐标为（x，x），表示出D的坐标，将C、D两点坐标代入反比例函数的解析式，解关于x的方程求出x即可得到点C、D的坐标，进而求得直线CD的解析式，最后计算该直线与y轴交点坐标即可得出结果．

解：作CE⊥x轴于点E，则∠CEO=90°，

过B作BF⊥x轴于F，过D作DM⊥x轴于M，则BF=CE，DM∥BF，BF=CE，

∵D为AB的中点，

∴AM=FM，

∴DM=BF，

∵∠COA=60°，

∴∠OCE=30°，

∴OC=2OE，CE=OE，

∴设C的坐标为（x，x），

∴AF=OE=x，CE=BF=x，OE=AF=x，DM=x，

∵四边形OABC是平行四边形，A（3，0），

∴OF=3+x，OM=3+x，

即D点的坐标为（3+x，x），

把C、D的坐标代入y=得：k=xx=（3+x）x，

解得：x1=2，x2=0（舍去），

∴C（2，2），D（4，），

设直线CD解析式为：y=ax+b，则

，

解得，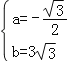

∴直线CD解析式为y=﹣x+3，

∴当x=0时，y=3，

∴E（0，3），即OE=3．

故答案为：3