
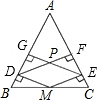
 如图,在△ABC中,AB=AC,M是BC的中点,分别作MD⊥AB于D,ME⊥AC于E,DF⊥AC于F,EG⊥AB于G,DF、EG相交于点P,求证:四边形DMEP是菱形.
如图,在△ABC中,AB=AC,M是BC的中点,分别作MD⊥AB于D,ME⊥AC于E,DF⊥AC于F,EG⊥AB于G,DF、EG相交于点P,求证:四边形DMEP是菱形. 分析 先求出四边形是平行四边形,证三角形全等,得出DM=ME,根据菱形的判定得出即可.
解答 证明:∵DF⊥AC、MF⊥AC,
∴DF∥ME,
同理,EG∥MD,
∴四边形DMEP是平行四边形,
∵AB=AC,
∴∠B=∠C,
∴在△BMD和△CME中,$\left\{\begin{array}{l}{∠MDB=∠MEC}\\{∠B=∠C}\\{BM=CM}\end{array}\right.$,
∴△BMD≌△CME,
∴MD=MF,
∴四边形DMEP是菱形.
点评 本题考查了全等三角形的性质和判定,菱形的判定,平行四边形的判定的应用,主要考查学生的推理能力,注意:有一组邻边相等的平行四边形是菱形.


科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:填空题
将函数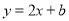 (b为常数)的图象位于
(b为常数)的图象位于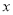 轴下方的部分沿
轴下方的部分沿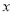 轴翻折至其上方后,所得的折线是函数
轴翻折至其上方后,所得的折线是函数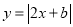 (b为常数)的图象.若该图象在直线y=2下方的点的横坐标
(b为常数)的图象.若该图象在直线y=2下方的点的横坐标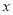 满足
满足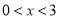 ,则b的取值范围为____.
,则b的取值范围为____.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
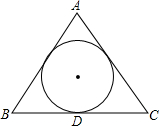 如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )
如图所示.在等边△ABC中,△ABC的内切圆半径是3,则△ABC的周长为( )| A. | 9$\sqrt{3}$ | B. | 18 | C. | 18$\sqrt{3}$ | D. | 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
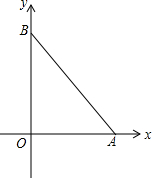 如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.
如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
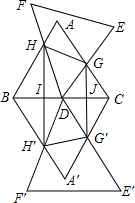 如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$cm,∠C=30°,点D从点C出发沿CA方向以每秒2cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$cm,∠C=30°,点D从点C出发沿CA方向以每秒2cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com