
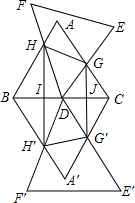
 如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.分析 (1)由等边三角形的特点得到相等关系,即可;
(2)由相似三角形得到$\frac{CG}{BD}=\frac{CD}{BH}$,再结合对称,表示出相关的线段,四边形HH′G′G的面积为y求出即可.
解答 证明:(1)在正△ABC中,∠ABC=∠ACB=60°,
∴∠BHD+∠BDH=120°,
在正△DEF中,∠EDF=60°,
∴∠GDC+∠BDH=120°,
∴∠BHD=∠GDC,
∴△DHB∽△GDC,
(2)①∵D为BC的中点,
∴BD=CD=2,
由△DHB∽△GDC,
∴$\frac{CG}{BD}=\frac{CD}{BH}$,
即:$\frac{x}{2}=\frac{2}{BH}$,
∴BH=$\frac{4}{x}$,
∵H,H′和G,G′关于BC对称,
∴HH′⊥BC,GG′⊥BC,
∴在Rt△BHI中,BI=$\frac{1}{2}$BH=$\frac{2}{x}$,HI=$\frac{\sqrt{3}}{2}$BH=$\frac{2}{x}$$\sqrt{3}$,
在Rt△CGJ中,CJ=$\frac{1}{2}$CG=$\frac{x}{2}$,GJ=$\frac{\sqrt{3}}{2}$CG=$\frac{x}{2}$$\sqrt{3}$,
∴HH′=2HI=$\frac{4}{x}\sqrt{3}$,GG’=2GJ=$\sqrt{3}$x,IJ=4-$\frac{2}{x}$-$\frac{x}{2}$,
∴y=$\frac{1}{2}$($\frac{4}{x}\sqrt{3}$+$\sqrt{3}$x)(4-$\frac{2}{x}$-$\frac{x}{2}$) ∵边DF、DE始终分别交△ABC的边AB、AC于点H、G,
∵边DF、DE始终分别交△ABC的边AB、AC于点H、G,
∴当△DEF绕点D旋转时,点H和A重合时,AG=3,
∴x=CG=1,
当点G和A重合时,CG=4,
∴x=4,
∴1≤x≤4
②由①得,y=-$\frac{\sqrt{3}}{4}$($\frac{4}{x}$+x)2+2$\sqrt{3}$($\frac{4}{x}$+x),
设$\frac{4}{x}+x$=a,得y=-$\frac{\sqrt{3}}{4}$a2+2$\sqrt{3}$a,
当a=4时,y最大=4$\sqrt{3}$,
此时$\frac{4}{x}+x$=4,解得x=2.
点评 此题是几何变换综合题,主要考查相似三角形的性质和判定以及对称的性质,用x表示线段是解决本题的关键,也是难点.


科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
地球上的陆地而积约为149000000km2.将149000000用科学记数法表示为( )
A. 1.49×106 B. 1.49×107 C. 1.49×108 D. 1.49×109
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
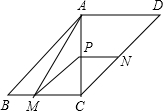 如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.
如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发,沿AC向终点C移动,过点P分别作PM∥AB,交BC于M,PN∥AD,交DC于N.连结AM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
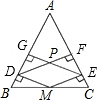 如图,在△ABC中,AB=AC,M是BC的中点,分别作MD⊥AB于D,ME⊥AC于E,DF⊥AC于F,EG⊥AB于G,DF、EG相交于点P,求证:四边形DMEP是菱形.
如图,在△ABC中,AB=AC,M是BC的中点,分别作MD⊥AB于D,ME⊥AC于E,DF⊥AC于F,EG⊥AB于G,DF、EG相交于点P,求证:四边形DMEP是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com