
分析 (1)首先计算乘方,然后计算乘法,求出算式m3•m•(m2)3 的值是多少即可.
(2)根据同底数幂的乘法法则,求出(p-q)4÷(q-p)3•(p-q)2的值是多少即可.
(3)首先计算乘方,然后计算乘法,最后计算减法,求出算式(-3a3)3-a5•(-3a2)2的值是多少即可.
(4)首先计算乘方,然后计算除法,最后从左向右依次计算,求出算式22-(-2)-2-32÷(3.14-π)0的值是多少即可.
解答 解:(1)m3•m•(m2)3
=m4•m6
=m10
(2)(p-q)4÷(q-p)3•(p-q)2
=(p-q)4÷[-(p-q)3]•(p-q)2
=-(p-q)3
(3)(-3a3)3-a5•(-3a2)2
=-27a9-a5•(9a4)
=-27a9-9a9•
=-36a9
(4)22-(-2)-2-32÷(3.14-π)0
=4-$\frac{1}{4}$-9÷1
=3$\frac{3}{4}$-9
=-5$\frac{1}{4}$
点评 (1)此题主要考查了整式的混合运算,要熟练掌握,解答此类问题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$ (a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(4)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
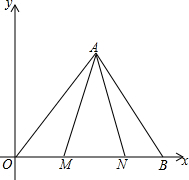 如图1,在平面直角坐标系中,已知A(a,a),B(2a,0),M($\frac{1}{2}$a,0),∠MAN=45°,将△OAM绕A逆时针旋转90°.
如图1,在平面直角坐标系中,已知A(a,a),B(2a,0),M($\frac{1}{2}$a,0),∠MAN=45°,将△OAM绕A逆时针旋转90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
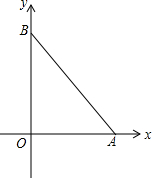 如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.
如图,在平面直角坐标系中,已知点A(3,0),点B(0,4),将线段AB绕点A按顺时针方向旋转得线段AB1,已知BB1和x轴平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
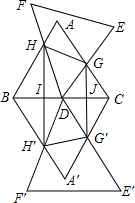 如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E、F分别是?ABCD的边BC、AD上的点,AE平分∠BAC、CF平分∠ACD.
如图,点E、F分别是?ABCD的边BC、AD上的点,AE平分∠BAC、CF平分∠ACD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com