
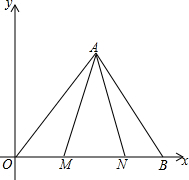
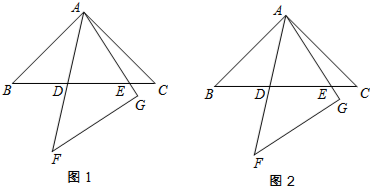
 如图1,在平面直角坐标系中,已知A(a,a),B(2a,0),M($\frac{1}{2}$a,0),∠MAN=45°,将△OAM绕A逆时针旋转90°.
如图1,在平面直角坐标系中,已知A(a,a),B(2a,0),M($\frac{1}{2}$a,0),∠MAN=45°,将△OAM绕A逆时针旋转90°.分析 (1)过点A作AH⊥x轴于H,根据A、B的坐标,证明AH=OH=BH即可;
(2)△EAN≌△MAN,再利用勾股定理计算出相关线段即可;
(3)利用勾股定理和角平分线的特点求出点P(0,-6).
解答 解:(1)如图1,△ABE为旋转后的图形,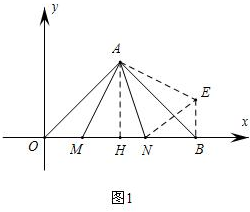
过点A作AH⊥x轴于H,
∵A(a,a),
∴OH=AH=a,
∵B(2a,0),
∴OB=2a,
∴BH=OH=a,
∵AH⊥x轴,
∴∠OHA=∠BHA=90°,
∴∠AOH=∠OAH=∠ABH=∠BAH=45°,
∴∠OAB=90°,OA=BA,
∴△OAB为等腰直角三角形;
(2)
由已知可得△ABE≌△AOM,
∴∠OAM=∠BAE,AE=AM,OM=BE,
∵∠ABE=∠AOM=45°,
∴∠EBN=90°,
∵∠OAM+∠BAM=90°,
∴∠BAE+∠BAM=90°,
∵∠MAN=45°,
∴∠EAN=45°,
连接NE,在△EAN和△MAN中,
$\left\{\begin{array}{l}{AN=AN}\\{∠MAN=∠EAN}\\{AM=AG}\end{array}\right.$,
∴△EAN≌△MAN(SAS),
∴MN=EN,
∵a=6,
∴OB=2a=12,OM=$\frac{1}{2}a$=3,
设BN=x,则MN=EN=12-3-x=9-x,
∵BN2+BG2=NG2,
∴x2+32=(9-x)2,
解得:x=4,
∴$\frac{{S}_{△OAM}}{{S}_{△BAN}}=\frac{\frac{1}{2}OM•AH}{\frac{1}{2}BN•AH}=\frac{OM}{BN}=\frac{3}{4}$;
(3)
存在P使PM平分∠OPN,如图2,过M作MQ⊥PN于Q,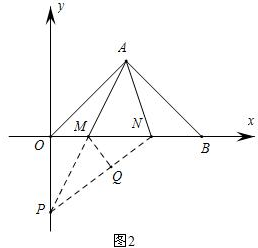
∵PM平分∠OPN,∠NOP=90°,
∴OM=MQ=3,
∵MN=9-x=9-4=5,∠MQN=90°,
∴NQ=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵∠MPO=∠MPQ,
∠MPO+∠OMP=90°,
∠MPQ+∠QMP=90°,
∴∠OMP=∠QMP,
∴OP=QP,
设OP=QP=m,则PN=4+m,
在Rt△OPN中,
∵OP2+ON2=PN2,
∴m2+82=(m+4)2,
解得:m=6,
∴P(0,-6),
∴存在P(0,-6)使PM平分∠OPN.
点评 此题是几何变换综合题,主要考查全等三角形判定和性质及旋转的特点,勾股定理的应用是解本题的关键,辅助线的作法是本题的难点.


科目:初中数学 来源:2017届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D,E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )
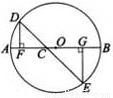
A. 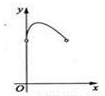 B.
B. 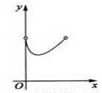 C.
C. 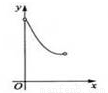 D.
D. 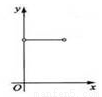
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
地球上的陆地而积约为149000000km2.将149000000用科学记数法表示为( )
A. 1.49×106 B. 1.49×107 C. 1.49×108 D. 1.49×109
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com