
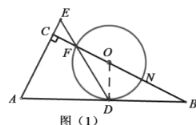
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 上一点
上一点![]() 为圆心作圆与
为圆心作圆与![]() 切于点
切于点![]() ,与
,与![]() 分别交于点
分别交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() ;
;
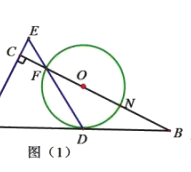
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
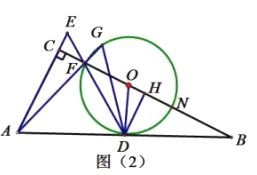
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 交
交![]() 的延长交于点
的延长交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
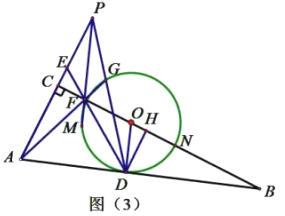
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据切线的性质可得![]() ,然后再根据等角的余角相等求得
,然后再根据等角的余角相等求得![]() ,再由等腰三角形的性质可得
,再由等腰三角形的性质可得![]() ;
;
(2)根据全等三角形的判定和性质及等腰三角形的性质可得![]() ,再由圆的内接四边形对角互补的性质和圆周角定理可得
,再由圆的内接四边形对角互补的性质和圆周角定理可得![]() ,再由等弧对应的圆周角相等求得
,再由等弧对应的圆周角相等求得![]() ,从而
,从而![]() 得证;
得证;
(3)由全等三角形的判定和性质及等腰三角形的性质可得![]() ,
,![]() ,从而可得
,从而可得![]() ,再根据题意证明
,再根据题意证明![]() 从而可得
从而可得![]() ,根据等角的正切值相等可求得RD,HN,进而可求得OF和OH.
,根据等角的正切值相等可求得RD,HN,进而可求得OF和OH.
![]() 连接
连接![]() 是
是![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
![]() 延长
延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
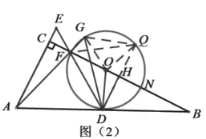
![]() 平分
平分![]() ,
,
![]() 同理
同理![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]()
∴![]() ,
,
![]() 是
是![]() 的直径,
的直径,![]() ,∴弧
,∴弧![]() 等于弧
等于弧![]() ,
,
![]() ;
;
![]() 延长
延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
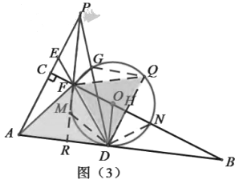
由![]() 知,
知,![]() ,
,
由![]() 知,
知,![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
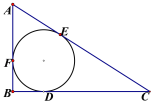
【题目】如图, Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F, (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r=![]() (a+b-c).
(a+b-c).
(2) 若AD交圆于P, PC交圆于H, FH//BC, 求∠CPD;
(3)若r=3![]() , PD=18, PC=27
, PD=18, PC=27![]() . 求△ABC各边长.
. 求△ABC各边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
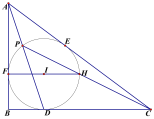
【题目】某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为10的半圆形量角器中,而一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是
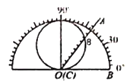
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将连续的奇数1,3,5,7…按如图中的方式排成一个数,用一个十字框框住5个数,这样框出的任意5个数中,四个分支上的数分别用a,b,c,d表示,如图所示.

(1)计算:若十字框的中间数为17,则a+b+c+d=______.
(2)发现:移动十字框,比较a+b+c+d与中间的数.猜想:十字框中a、b、c、d的和是中间的数的______;
(3)验证:设中间的数为x,写出a、b、c、d的和,验证猜想的正确性;
(4)应用:设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
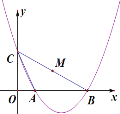
A. n=![]() (m-
(m-![]() )2-
)2-![]() B. n=
B. n=![]() (m-
(m-![]() )2+
)2+![]()
C. n=![]() (m-
(m-![]() )2-
)2-![]() D. n=
D. n=![]() (m-
(m-![]() )2-
)2-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com