
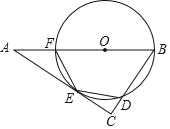
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
科目:初中数学 来源: 题型:
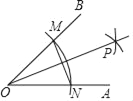
【题目】已知∠AOB=45°,求作∠AOP=22.5°,作法:
(1)以O为圆心,任意长为半径画弧分别交OA,OB于点N,M;
(2)分别以N,M为圆心,以OM长为半径在角的内部画弧交于点P;
(3)作射线OP,则OP为∠AOB的平分线,可得∠AOP=22.5°
根据以上作法,某同学有以下3种证明思路:
①可证明△OPN≌△OPM,得∠POA=∠POB,可得;
②可证明四边形OMPN为菱形,OP,MN互相垂直平分,得∠POA=∠POB,可得;
③可证明△PMN为等边三角形,OP,MN互相垂直平分,从而得∠POA=∠POB,可得.
你认为该同学以上3种证明思路中,正确的有( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
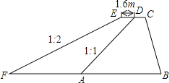
【题目】如图,开发区为提高某段海堤的防潮能力,将长![]() 的一堤段(原海堤的横断面如图中的梯形
的一堤段(原海堤的横断面如图中的梯形![]() )的堤面加宽
)的堤面加宽![]() ,将原来的背水坡度
,将原来的背水坡度![]() (坡比
(坡比![]() )改成现在的背水坡(坡比
)改成现在的背水坡(坡比![]() ),已知
),已知![]() ,求完成这一工程所需的土方.
,求完成这一工程所需的土方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的
有两个实数根,且其中一个根为另一个根的![]() 倍,那么称这样的方程为“倍根方程”,例如,一元二次方程
倍,那么称这样的方程为“倍根方程”,例如,一元二次方程![]() 的两个根是
的两个根是![]() 和
和![]() ,则方程
,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() = .
= .
(2)若关于![]() 的一元二次方程
的一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() ,
,![]() ,
,![]() 之间的关系为 .
之间的关系为 .
(3)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
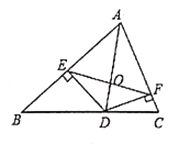
【题目】如图,![]() 为
为![]() 的角平分线,
的角平分线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
探究:判断![]() 的形状,并说明理由;
的形状,并说明理由;
发现:![]() 与
与![]() 之间有怎样的数量关系,请直接写出你的结论,不必说明理由.
之间有怎样的数量关系,请直接写出你的结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
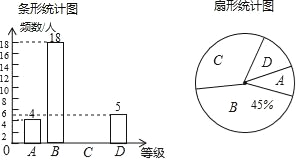
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
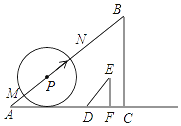
【题目】如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
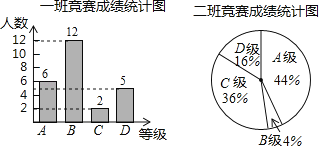
【题目】在学校组织的八年级数学竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据提供的信息解答下列问题:
(1)此次竞赛中二班80分以上(包括80分)的人数为 ;
(2)请你将表格补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 77.6 | 80 |
|
二班 | 77.6 |
| 90 |
(3)请从不同角度对这次竞赛成绩的结果进行分析.(至少两个角度)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com