
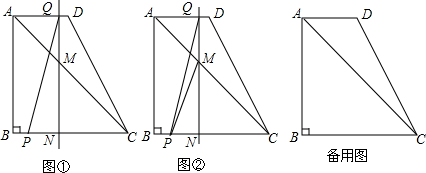
���� ��1����QD=t��BP=2t�������õ���ֱ�������κ����Ǻ��������ʽ��н�ɣ�
��2������ƽ���ı��ε����ʽ��н�ɣ�
��3�����������ε������ʽ��һԪ���η��̵Ľⷨ���н�ɣ�
��4��������������õ��������ε����ʽ��н�ɣ�
��� �⣺��1���������֪��QD=t��BP=2t��
AQ=2-t=BN��
��NC=4-��2-t��=t+2��
�ߡ�B=90�㣬AB=CB��
���BCA=45�㣬
��MC=$\frac{NC}{cos45��}=\sqrt{2}$��t+2��=$\sqrt{2}$t+2$\sqrt{2}$��
��2�����ı���PCDQΪƽ���ı��Σ�
��PC=DQ��
��BP=2t��
��PC=4-2t��
��4-2t=t��
��ã�t=$\frac{4}{3}$��
��t=$\frac{4}{3}$��ʱ���ı���PCDQΪƽ���ı��Σ�
��3�������ڣ��������£�
����QNƽ���ˡ�ABC�����
��$\frac{1}{2}N{C}^{2}=\frac{1}{2}��\frac{1}{2}B{C}^{2}$����$\frac{1}{2}��t+2��^{2}=\frac{1}{2}��\frac{1}{2}��{4}^{2}$��
��ã�${t}_{1}=2\sqrt{2}-2��{t}_{2}=-2\sqrt{2}-2$���ᣩ��
��ʱ��NC=$2\sqrt{2}$��MC=8��BN=4-2$\sqrt{2}$��AM=$4\sqrt{2}$-8��
��BN+AB+AM=4-$2\sqrt{2}$+4+$4\sqrt{2}$-8=$2\sqrt{2}$��
MC+NC=8+$2\sqrt{2}$��
��BN+AB+AM��MC+NC��
�����ij��ʱ��ʹ��ֱ��QNͬʱƽ�֡�ABC���ܳ��������
��4����t=0����PMC����������
��t=$6-4\sqrt{2}$����PMC����������
��t=$\frac{2}{3}$����PMC����������
���� ������Ҫ�������ֱ�������ε����ʡ�ƽ���ı��ε����ʣ��ڽ��⣨3��ʱ��Ӧע�������������ۣ���ֹ�ڽ�������г���©������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B�� | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ | C�� | $\sqrt{��-3��^{2}}$=-3 | D�� | -1-1=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | -2 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��AB=CD��AB��CD��DE��AC��BF��AC��E��F�Ǵ��㣬AF=5����CE�ij���
��֪����ͼ��AB=CD��AB��CD��DE��AC��BF��AC��E��F�Ǵ��㣬AF=5����CE�ij����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com