
已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
(1)求证:BF与⊙O相切;
(2)若BF=5,cosC=
 ,求⊙O的半径.
,求⊙O的半径.


【考点】切线的判定.
【分析】(1)连接BD,证明BF是⊙O的切线,只需证明∠FBD=90°;
(2)由Rt△BDF中的勾股定理进行解答即可.
【解答】证明:(1)连接BD,
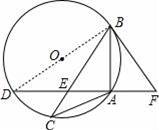

∵AD⊥AB,
∴∠BAD=90°,
∴BD是直径,BD过圆心,
∵AB=AC,
∴∠ABC=∠D,
又∵∠C=∠D,
∴△BEF是等腰三角形,
∴∠ABC=∠ABF,
∴∠D=∠ABF,
又∵∠BAD=90°,
∴∠ABD+∠D
=180°﹣∠BAD
=180°﹣90°
=90°,
∴∠ABD+∠ABF=90°,
∴∠DBF=90°,
∴OB⊥BF,
又∵OB是⊙O的半径,
∴BF是⊙OA切线;
(2)∵∠C=∠D,
∴cosD=cosC=
 ,
,
在Rt△BDF中
cosD=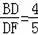
 ,
,
∴设BD=4x,DF=5x,
又∵BD2+DF2=DF2
∴(4x)2+52=(5x)2
x=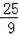
 ,
,
∵x>0
∴x=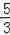
 ,
,
∴BD=4×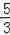
 =
=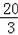
 ,
,
∴OB=
 BD=
BD=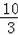

∴⊙O半径为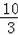
 .
.
【点评】本题考查圆的切线的判断,关键是证明∠FBD=90°来证明BF是⊙O的切线.


科目:初中数学 来源: 题型:
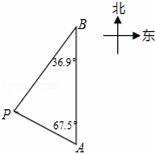
日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图,上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°方向,海检船以21海里/时 的速度向正北方向行驶,下午2时海检船到达B处,这时观察到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P的距离?
(参考数据: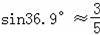
 ,
,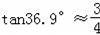
 ,
,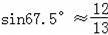
 ,
,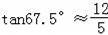
 )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com