
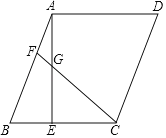
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
【答案】(1)![]() 1;(2)见解析.
1;(2)见解析.
【解析】
(1)在Rt△ABE中,由勾股定理求得BE,再由线段和差求得结果;
(2)延长GA到H,使得AH=BE,证明△ADH≌△EAB得DH=AB=CD,得∠DCH=∠DHC,再证明∠GHC=∠GCH得GC=GH便可得结果.
(1)∵CF=CB=AE,BC![]() ,
,
∴AE![]() ,
,
∵AE⊥BC于点E,AB![]() ,
,
∴BE![]() ,
,
∴CE=BC﹣BE![]() 1;
1;
(2)延长GA到H,使得AH=BE,连接DH,CH,
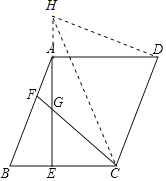
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE⊥BC,
∴∠AEB=∠DAE=90°,
∵BC=AE,
∴AE=DA,
在△ADH和△EAB中,
 ,
,
∴△ADH≌△EAB(SAS),
∴DH=DC,∠DHA=∠ABE,
∴∠DHC=∠DCH,
∵CB=CF,
∴∠CBF=∠CFB,
∵AB∥CD,
∴∠CFB=∠DCF,
∴∠CBF=∠DCF,
∵∠DHA=∠ABE,
∴∠DHA=∠DCF,
∵∠DHC=∠DCH,
∴∠CHG=∠HCG,
∴CG=HG,即CG=AG+AH,
∴AH=CG﹣AG,
∵AH=BE,
∴BE=CG﹣AG,


科目:初中数学 来源: 题型:
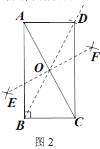
【题目】以点A为顶点作等腰Rt△ABC,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE,延长BD交CE于点F.

(1)试判断BD、CE的关系,并说明理由;
(2)把两个等腰直角三角形按如图2所示放置,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在直线l外,点B在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
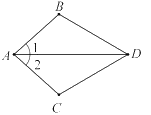
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)![]() 的值为 ________.
的值为 ________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低![]() 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含![]() 的代数式表示);
的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学课上,老师布置了一个任务:
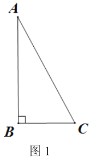
已知,如图1,在![]() 中,
中,![]() ,用尺规作图作矩形
,用尺规作图作矩形![]() .
.
同学们开动脑筋,想出了很多办法,其中小亮作了图2,他向同学们分享了作法:
①分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧分别交于点
长为半径画弧,两弧分别交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ;
;
②作射线![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ;
;
③连接![]() ,
,![]() .
.
则四边形![]() 就是所求作的矩形.
就是所求作的矩形.
老师说:“小亮的作法正确.”
写出小亮的作图依据.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com