
【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)![]() 的值为 ________.
的值为 ________.

科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=x-3交x轴于点B,交y轴于点C,抛物线经过点A(-1,0),B,C三点,点F在y轴负半轴上,OF=OA.
(1)求抛物线的解析式;
(2)在第一象限的抛物线上存在一点P,满足S△ABC=S△PBC,请求出点P的坐标;
(3)点D是直线BC的下方的抛物线上的一个动点,过D点作DE∥y轴,交直线BC于点E,①当四边形CDEF为平行四边形时,求D点的坐标;
②是否存在点D,使CE与DF互相垂直平分?若存在,请求出点D的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
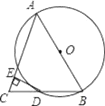
【题目】如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分6分)
(1)(3分)(-3)2-|-![]() |+(3.14-x)0
|+(3.14-x)0
(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
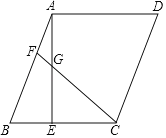
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
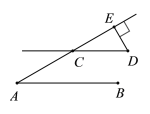
【题目】(1)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=30°,求∠D的度数.
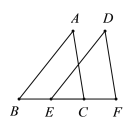
(2)如图,E,C在BF上,AB=DE,AC=DF,BE=CF,试说明:AC∥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用大小相等的小正方形按一定规律拼成的,则第10个图形是_________个小正方形,第n 个图形是___________个小正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
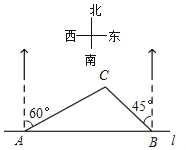
【题目】如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____千米.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com