
【题目】以点A为顶点作等腰Rt△ABC,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE,延长BD交CE于点F.

(1)试判断BD、CE的关系,并说明理由;
(2)把两个等腰直角三角形按如图2所示放置,(1)中的结论是否仍成立?请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线![]() 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
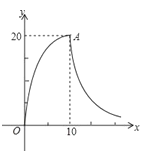
【题目】最近流感高发期,在预防流感期间学校坚持天天消毒,下图是某次消毒时教室内空气中消毒液浓度 y(单位:毫克/立方米)随时间 x(单位:分钟)的变化情况图.从开始喷药到喷药结束的 10 分钟内(包括第十分钟),y 是 x 的二次函数;喷药结束后(从第十分钟开始),y 是 x 的反比例函数.
(1)如果点 A 是图中二次函数的顶点,求二次函数和反比例函数的解析式 (要写出自变量取值范围);
(2)已知空气中消毒液浓度 y 不少于 15 毫克/立方米且持续时间不少于 8 分钟才能有效消毒,通过计算,请你回答这次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去等加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,
若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新特动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果![]() ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
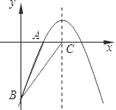
【题目】如图,已知二次函数y=﹣![]() +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)求当x满足什么条件时,函数值大于0?;
(3)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
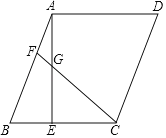
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com