
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点(点A在点B的左侧).
(Ⅰ)求出点A、B的坐标;
(Ⅱ)当a<0时,经过点A的直线l:y=kx+a与y轴负半轴交于点C,与抛物线的另一个交点为D,点E是抛物线上的一个动点,且在直线l上方.
①若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
②设P是抛物线的对称轴上的一点,点Q在抛物线上,当以点A、D、P、Q为顶点的四边形构成矩形时,请直接写出此时点P的坐标.
【答案】(Ⅰ)A(﹣1,0),B(3,0);(Ⅱ)①﹣![]() ;②P1(1,﹣4),P2(1,﹣
;②P1(1,﹣4),P2(1,﹣![]() ).
).
【解析】
(Ⅰ)令y=0,则ax2﹣2ax﹣3a=0,可求点A、B的坐标;
(Ⅱ)①先求直线l的解析式,点E(m,am2﹣2am﹣3a),求出直线AE解析式,由三角形的面积公式可求△ACE的面积=![]() ×(m﹣
×(m﹣![]() )2﹣
)2﹣![]() a,即可求解;
a,即可求解;
②分以AD为边或对角线两种情况讨论即可.
解:(Ⅰ)令y=0,则ax2﹣2ax﹣3a=0,
解得x1=﹣1,x2=3
∵点A在点B的左侧,
∴A(﹣1,0),B(3,0)
(Ⅱ)①∵直线l:y=kx+a经过点A,
∴0=﹣k+a,
∴k=a,
∴直线l:y=ax+a,
如图1,过点E作EN⊥y轴,垂足为N,设AE与y轴的交点为M,

设点E(m,am2﹣2am﹣3a),yAE=k1x+b,
则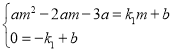 ,
,
解得:![]() ,
,
∴yAE=(am﹣3a)x+am﹣3a,M(0,am﹣3a)
∵MC=am﹣3a﹣a=am﹣4a,NE=m
∴S△ACE=S△ACM+S△CEM=![]() [am﹣4a]×1+
[am﹣4a]×1+![]() [am﹣4a]m=
[am﹣4a]m=![]() ×(m﹣
×(m﹣![]() )2﹣
)2﹣![]() a,
a,
∵a<0,
∴最大值﹣![]() a=
a=![]() ,
,
∴a=﹣![]() ;
;
②令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,
解得x1=﹣1,x2=4,
∴D(4,5a),
∵y=ax2﹣2ax﹣3a,
∴抛物线的对称轴为x=1,
设P1(1,m),
如图2,若AD是矩形的一条边,
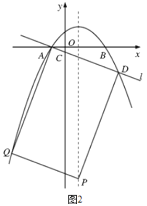
由AQ∥DP知xD﹣xP=xA﹣xQ,可知Q点横坐标为﹣4,将x=﹣4代入抛物线方程得Q(﹣4,21a),
m=yD+yQ=21a+5a=26a,则P(1,26a),
∵四边形ADPQ为矩形,∴∠ADP=90°,
∴AD2+PD2=AP2,
∵AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,
PD2=(1﹣4)2+(26a﹣5a)2=32+(21a)2,
∴[4﹣(﹣1)]2+(5a)2+(1﹣4)2+(26a﹣5a)2=(﹣1﹣1)2+(26a)2,
即a2=![]() ,
,
∵a<0,
∴a=﹣![]() ,
,
∴P1(1,﹣![]() ).
).
如图3,若AD是矩形的一条对角线,

则线段AD的中点坐标为(![]() ,
,![]() ),Q(2,﹣3a),
),Q(2,﹣3a),
m=5a﹣(﹣3a)=8a,则P(1,8a),
∵四边形AQDP为矩形,∴∠APD=90°,
∴AP2+PD2=AD2,
∵AP2=[1﹣(﹣1)]2+(8a)2=22+(8a)2,
PD2=(4﹣1)2+(8a﹣5a)2=32+(3a)2,
AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,
∴22+(8a)2+32+(3a)2=52+(5a)2,
解得a2=![]() ,
,
∵a<0,
∴a=﹣![]() ,
,
∴P2(1,﹣4).
综上可得,P点的坐标为P1(1,﹣4),P2(1,﹣![]() ).
).


科目:初中数学 来源: 题型:
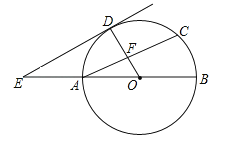
【题目】如图,AB为⊙O的直径,D为![]() 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)连接CD,若OA=AE=4,求四边形ACDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市居民用水情况,在某小区随机抽查了20户家庭,并将这些家庭的月用水量进行统计,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 13 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法正确的是( )
A.中位数是5B.平均数是5C.众数是6D.方差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知二次函数y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b2<4ac;③4a+2b+c>0;④2a+b=0;⑤a+b<m(am+b)(m≠1的实数),其中结论正确的个数有( )
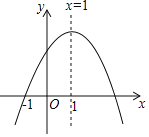
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
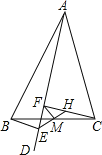
A.M是BC的中点B.FM=![]() EH
EH
C.CF⊥ADD.FM⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
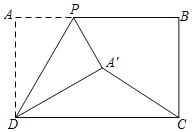
【题目】如图,点P为矩形ABCD的AB边上一动点,将△ADP沿着DP折叠,点A落在点A'处,连接CA',已知AB=10,AD=6,若以点P,B,C,A'为端点的线段(不再另外连接线段)构成的图形为直角三角形或特殊的平行四边形时,AP的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com