
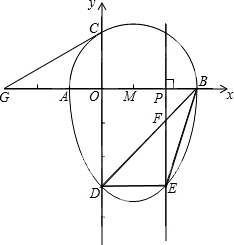
 ���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2������Բ����ƽ����y���ֱ�߽صõ�����ҳ�6��
���ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2������Բ����ƽ����y���ֱ�߽صõ�����ҳ�6������ ��1������M��GH��y�ᣬ������Բ����N��H����ͼ����GH=6������NM=2��M��1��0������H��1��-4���������ð�ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��ȷ��A��-1��0����B��3��0�������ǿ����ý���ʱ���
����Բ�������߲��ֵĽ���ʽΪy=x2-2x-3��-1��x��3����
��2��������CM����ͼ����Rt��OCM�����ù��ɶ��������OC=$\sqrt{3}$������y���ϵ����������ȷ��D��0��-3������OD=3������CD=$\sqrt{3}$+3��
������GC�С���Բ���İ�Բ��C���������ߵ����ʵá�MCG=90�㣬���ݺ�30��ֱ�����������߹�ϵ����OM=1��MC=2�õ���MCO=30�㣬�����õȽǵ������ȵá�CGM=30�㣬����MG=2MC=4����G��-3��0����
��3�������ô���ϵ�������ֱ��BD�Ľ���ʽΪy=x-3����E��x��x2-2x-3������F��x��x-3��������EF=-x2+3x�����������������ʽ��S��BDE=S��DEF+S��BEF=$\frac{1}{2}$•EF•OB=$\frac{1}{2}$•3•��-x2+3x��=-$\frac{3}{2}$x2+$\frac{9}{2}$x��Ȼ����ݶ��κ��������ʽ�����⣮
��� �⣺��1������M��GH��y�ᣬ������Բ����N��H����ͼ����GH=6��
��NM=2��
��MH=4��
��M��1��0����
��H��1��-4����
�߰�ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��
��A��-1��0����B��3��0����
�衰��Բ�������߲��ֵĽ���ʽΪy=a��x+1����x-3����
��H��1��-4�������a•2•��-2��=-4�����a=1��
�ࡰ��Բ�������߲��ֵĽ���ʽΪy=��x+1����x-3����
��y=x2-2x-3��-1��x��3����
��2��������CM����ͼ��
��Rt��OCM����OM=1��MC=2��
��OC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$��
��x=0ʱ��y=x2-2x-3=-3����D��0��-3����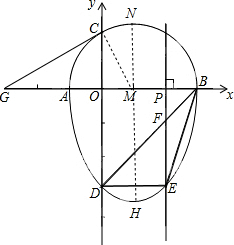
��OD=3��
��CD=OC+OD=$\sqrt{3}$+3��
�ʴ�Ϊ$\sqrt{3}$+3��
�ڡ�GC�С���Բ���İ�Բ��C��
��MC��CG��
���MCG=90�㣬
��OM=1��MC=2��
���MCO=30�㣬
���CGM=30�㣬
��MG=2MC=4��
��OG=GM-OM=4-1=3��
��G��-3��0����
��3�����ڣ�
��ֱ��BD�Ľ���ʽΪy=kx+b��
��B��3��0����D��0��-3�������$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪy=x-3��
��E��x��x2-2x-3����
��PE��x�ᣬ
��F��x��x-3����
��EF=x-3-��x2-2x-3��=-x2+3x��
��S��BDE=S��DEF+S��BEF=$\frac{1}{2}$•EF•OP+$\frac{1}{2}$EF•BP=$\frac{1}{2}$•EF•OB=$\frac{1}{2}$•3•��-x2+3x��=-$\frac{3}{2}$x2+$\frac{9}{2}$x=-$\frac{3}{2}$��x-$\frac{3}{2}$��2+$\frac{27}{8}$��
�൱x=$\frac{3}{2}$ʱ��S��BDE�����ֵ�����ֵΪ$\frac{27}{8}$��
��ʱE������Ϊ��$\frac{3}{2}$��-$\frac{15}{4}$����
���� ���⿼���˶��κ����ۺ��⣺�������ն��κ���ͼ����һ�κ���ͼ���ϵ���������������κ��������ʺ����ߵ����ʣ������ô���ϵ������������ʽ������������ͼ�����ʣ����ź�30�ȵ�ֱ�����������ߵĹ�ϵ��


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
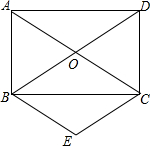 ��֪����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��BE��AC��CE��DB��
��֪����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��BE��AC��CE��DB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڽǺ͵���360�� | B�� | �Խ���� | ||
| C�� | �Խ���ƽ��һ��Խ� | D�� | �ڽǻ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
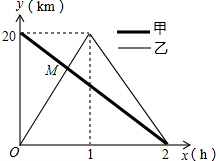 ��һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱx��h��֮��ĺ���ͼ����ͼ�����������⣺
��һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱx��h��֮��ĺ���ͼ����ͼ�����������⣺�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com