
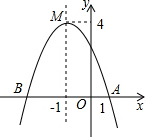 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )| A. | a<0 | B. | 当x=-1时,函数y有最小值4 | ||
| C. | 对称轴是直线=-1 | D. | 点B的坐标为(-3,0) |
分析 根据二次函数图象的开口向下可知a<0,对称轴为直线x=-1,当x=-1时,函数y有最大值4,再根据点A的坐标为(1,0)对称轴为直线x=-1,可得点B的坐标为(-3,0),由此以上信息可得问题答案.
解答 解:A、因为函数的图象开口向下,所以a<0,此选项说法不正确,故此选项不符合题意;
B、当x=-1时,函数y有最大值4,而不是最小值,此选项说法不正确,故该选项符合题意;
C、由函数的图象可知,抛物线对称轴是直线=-1,此选项说法不正确,故此选项不符合题意;
D、由点A的坐标为(1,0)对称轴为直线x=-1,可得点B的坐标为(-3,0),此选项说法不正确,故此选项不符合题意,
故选B.
点评 本题考查了抛物线和x轴的交点,解题的关键是熟练掌握象限内点的特点以及各类函数图象的图象特征.


科目:初中数学 来源: 题型:选择题
| 温度/℃ | 22 | 24 | 26 | 29 |
| 天数 | 2 | 1 | 3 | 1 |
| A. | 24,25 | B. | 25,26 | C. | 26,24 | D. | 26,25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
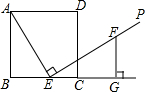 如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com