
【题目】如图,在长方形![]() 中,
中,![]() =4,
=4, ![]() =8,点
=8,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:① ![]() ;②当
;②当![]() 时,
时,![]() 平分
平分 ![]() ; ③△
; ③△![]() 周长的最小值为15 ;④当
周长的最小值为15 ;④当![]() 时,
时,![]() 平分
平分![]() .其中正确的个数有( )
.其中正确的个数有( )
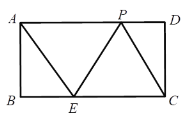
A.4个B.3个C.2个D.1个
【答案】B
【解析】
根据![]() ,可设BE=x,则AE=8-x,利用Rt△ABE中勾股定理即可求出BE;当
,可设BE=x,则AE=8-x,利用Rt△ABE中勾股定理即可求出BE;当![]() 时,四边形APCE为菱形,故可得到
时,四边形APCE为菱形,故可得到![]() 平分
平分 ![]() ;作C点关于直线AD的对称点C’,根据对称性即可求出△
;作C点关于直线AD的对称点C’,根据对称性即可求出△![]() 周长的最小值;过点A作AH⊥PE,PG⊥BC,根据
周长的最小值;过点A作AH⊥PE,PG⊥BC,根据![]() 求得DP、GC的长,再得到EG,故可求出BP的长,根据等面积法得到AH的长,由AH=AB即可证明
求得DP、GC的长,再得到EG,故可求出BP的长,根据等面积法得到AH的长,由AH=AB即可证明![]() 平分
平分![]() .
.
∵![]() ,设BE=x,则AE=8-x,
,设BE=x,则AE=8-x,
在Rt△ABE中AE2=AB2+BE2,
即(8-x)2=42+x2,
解得x=3,故① ![]() 正确;
正确;
当![]() 时,∵EC=5
时,∵EC=5
∴AP∥EC,AP=CE,
∴四边形APCE为平行四边形。
又AE=EC,
∴四边形APCE为菱形,
故可得到![]() 平分
平分 ![]() ,②正确;
,②正确;
作C点关于直线AD的对称点C’,则PC=PC’
∴△![]() 周长的最小值为EC+EC’=5+
周长的最小值为EC+EC’=5+![]() ,故③错误;
,故③错误;
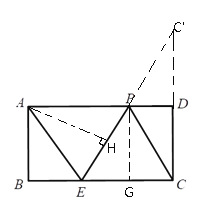
过点A作AH⊥PE,PG⊥BC,
∴AB=PG=4
∵![]()
∴PD=![]() =GC
=GC
∴EG=5-![]() =
=![]()
故EP=![]() =
=![]()
又S△AEP=![]() AP×PG=
AP×PG=![]() EP×AH
EP×AH
即![]() ×
×![]() ×4=
×4=![]() ×
×![]() ×AH
×AH
∴AH=4=AB,
∴![]() 平分
平分![]() ,④正确;
,④正确;
故选B.


科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
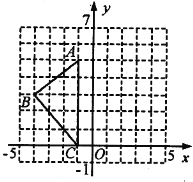
【题目】如图,在平面直角坐标系中,A(-1,5),B(-4,3),C(-1,0)
(1)在图中画出△ABC关于![]() 轴的对称图形△A1B1C1.
轴的对称图形△A1B1C1.
(2)写出点A1,B1,C1的坐标.
(3)计算四边形BCC1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 关于
关于![]() 的二次函数
的二次函数![]()
(1)当![]() 时,求该函数图像的顶点坐标.
时,求该函数图像的顶点坐标.
(2)在(1)条件下,![]() 为该函数图像上的一点,若
为该函数图像上的一点,若![]() 关于原点的对称点
关于原点的对称点![]() 也落在该函数图像上,求
也落在该函数图像上,求![]() 的值
的值
(3)当函数的图像经过点(1,0)时,若![]() 是该函数图像上的两点,试比较
是该函数图像上的两点,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。
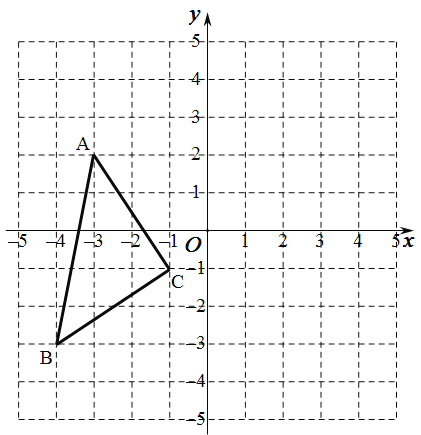
(1)写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△A2B2C2的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知R△ABDC中,∠C=90°,AD、BE是角平分线,它们相交于P,PF⊥AD于P交BC的延长线于F,交AC于H.
(1)求证:AH+BD=AB;
(2)求证:PF=PA.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com