
【题目】已知R△ABDC中,∠C=90°,AD、BE是角平分线,它们相交于P,PF⊥AD于P交BC的延长线于F,交AC于H.
(1)求证:AH+BD=AB;
(2)求证:PF=PA.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先计算出∠APB=135°,进而得到∠BPD=45°,然后再计算出∠FPB=135°,然后证明△ABP≌△FBP,得∠F=∠CAD,然后证明△APH≌△FPD,进而得到AH=FD,再利用等量代换可得结论.
(2)由△ABP≌△FBP可得PA=PF.
证明(1)∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=![]() (∠CAB+∠CBA)=45°,
(∠CAB+∠CBA)=45°,
∴∠APB=135°,
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
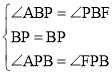 ,
,
∴△ABP≌△FBP(ASA),
∴∠BAP=∠F,
∵∠BAP=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
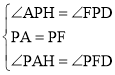 ,
,
∴△APH≌△FPD(ASA),
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.
(2)证明:由(1)可知△ABP≌△FBP,
∴PA=PF,


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
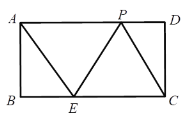
【题目】如图,在长方形![]() 中,
中,![]() =4,
=4, ![]() =8,点
=8,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:① ![]() ;②当
;②当![]() 时,
时,![]() 平分
平分 ![]() ; ③△
; ③△![]() 周长的最小值为15 ;④当
周长的最小值为15 ;④当![]() 时,
时,![]() 平分
平分![]() .其中正确的个数有( )
.其中正确的个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,工人师傅做一个矩形铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①所示),使![]() .
.
(2)摆放成如图②的四边形,则这时窗框的形状是平行四边形,它的依据是____________.
(3)将直尺紧靠窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是矩形,它的依据是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图是三个方向看到的一个几何体的形状.
(1)写出这个几何体的名称;
(2)写出它的侧面展开的形状;
(3)若从正面看到的高为10cm,从上面看到的三角形的三边长都为4cm,求这个几何体的侧面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明口袋中装有![]() 个红球、
个红球、![]() 个白球、
个白球、![]() 个黄球,每个球除颜色外其他均相同.从这个口袋中同时摸出两个球,发生概率最小的事件是摸到( )
个黄球,每个球除颜色外其他均相同.从这个口袋中同时摸出两个球,发生概率最小的事件是摸到( )
A. 都是红球 B. 一个红球,一个白球
C. 都是白球 D. 一个白球,一个黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据我囯古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三,股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5; 5,12,13; 7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且勾为3时,股![]() ,弦
,弦![]() ;勾为5时,股
;勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24=__________;弦25=___________.
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股=________;弦=_______.
的式子表示股和弦,则股=________;弦=_______.
(3)继续观察①4,3,5;②6,8,10;③8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.请你直接用![]() (
(![]() 为偶数且
为偶数且![]() )的代数式来表示直角三角形的另一条直角边和弦的长.
)的代数式来表示直角三角形的另一条直角边和弦的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图像如下图
所示:

(1)根据图像,直接写出y1、y2关于x的函数关系式;
(2)若两车之间的距离为S千米,请写出S关于x的函数关系式;
(3)甲、乙两地间有A、B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
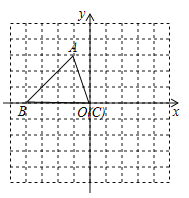
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在铁路线![]() 附近有两个村庄
附近有两个村庄![]() ,到铁路的距离分别是
,到铁路的距离分别是![]() 和
和![]() ,作
,作![]() ,垂足分别为
,垂足分别为![]() ,且
,且![]() 现在要在铁路线旁建一个农副产品站E,使得E地到A、B两地的距离相等.
现在要在铁路线旁建一个农副产品站E,使得E地到A、B两地的距离相等.
(1)请利用尺规作图确定站![]() 的位置.(不写作法,保留作图痕迹)
的位置.(不写作法,保留作图痕迹)
(2)求出![]() 长度.
长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com