
【题目】如图,在菱形ABCD中,∠A=60°,E,F分别是AB,AD的中点,DE,BF相交于点G,连接BD,CG.有下列结论:
①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD= ![]() AB2
AB2
其中正确的结论有( )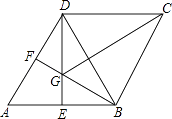
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:①由菱形的性质可得△ABD、BDC是等边三角形,∠DGB=∠GBE+∠GEB=30°+90°=120°,故①正确;
②∵∠DCG=∠BCG=30°,DE⊥AB,∴可得DG= ![]() CG(30°角所对直角边等于斜边一半)、BG=
CG(30°角所对直角边等于斜边一半)、BG= ![]() CG,故可得出BG+DG=CG,即②也正确;
CG,故可得出BG+DG=CG,即②也正确;
③首先可得对应边BG≠FD,因为BG=DG,DG>FD,故可得△BDF不全等△CGB,即③错误;
④S△ABD= ![]() ABDE=
ABDE= ![]() AB
AB ![]() BE=
BE= ![]() AB
AB ![]() AB=
AB= ![]() AB2 , 即④正确.
AB2 , 即④正确.
综上可得①②④正确,共3个.
故选C.
【考点精析】通过灵活运用菱形的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.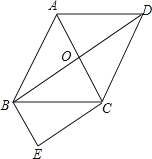
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1). 
①先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1 , 试在图中画出Rt△A1B1C1 , 并写出点B1的坐标;
②再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2 , 试在图中画出Rt△A2B2C2 . 并写出点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H.找出∠BHC和∠A之间存在何种等量关系;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?
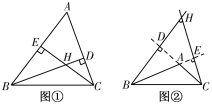
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24
(1)求CD的长;
(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. 
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系种中,点![]()
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于原点对称的点的坐标是:________;
关于原点对称的点的坐标是:________;
![]() 将点
将点![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕另一点
绕另一点![]() 旋转
旋转![]() 得到点
得到点![]() ,则
,则![]() 点的坐标为________.
点的坐标为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com