
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图l),求证:AE=CG; 
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段(不需要添加辅助线),并说明理由. 
【答案】
(1)解:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
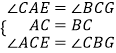 ,
,
∴△AEC≌△CGB(ASA),
∴AE=CG
(2)解:BE=CM.
理由:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,
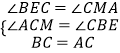 ,
,
∴△BCE≌△CAM(AAS),
∴BE=CM
【解析】(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG;(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列直线中,经过第一、二、三象限的是( )
A. 直线y= x-1 ; B. 直线y= -x+1; C. 直线y=x+1; D. 直线y=-x-1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=-![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.

(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式乘法中不能用平方差公式计算的是( )
A. (a3+b3)(a3﹣b3) B. (a2+b2)(b2﹣a2)
C. (2x2y+1)(2x2y﹣1) D. (x2﹣2y)(2x+y2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有两条线段AB和CD , 线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.![]()
(1)填空:点B在数轴上表示的数是 , 点C在数轴上表示的数是;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)约定“※”为一种新的运算符号,先观察下列各式:
1※3=1×4+3=7;3※(﹣1)=3×4﹣1=11;5※ ![]() =5×4+
=5×4+ ![]() =
= ![]() ;
;
5※4=5×4+4=24;4※(﹣3)=4×4﹣3=13;(﹣ ![]() )※0=(﹣
)※0=(﹣ ![]() )×4+0=﹣
)×4+0=﹣ ![]()
…
根据以上的运算规则,写出a※b= .
(2)根据(1)中约定的a※b的运算规则,求解问题①和②
①若(x﹣3)※x的值等于13,求x的值;
②若2m﹣n=2,请计算:(m﹣n)※(2m+n).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com