
【题目】如图,直角坐标系中,抛物线y=a(x﹣4)2﹣16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y=![]() x+b分别交x,y轴于点A,B.
x+b分别交x,y轴于点A,B.
(1)写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).
(2)若AF=AH=OH,求证:∠CEO=∠ABO.
(3)当b>﹣4时,以AB为边作正方形,使正方形的另外两个顶点一个落在抛物线上,一个落在抛物线的对称轴上,求所有满足条件的a及相应b的值.(直接写出答案即可)
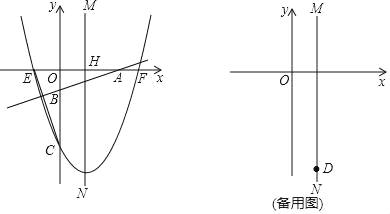
【答案】(1)D(4,﹣16),点C的纵坐标为16a﹣16;(2)见解析;(3)a=![]() ,b=﹣2或a=
,b=﹣2或a=![]() ,b=﹣1或a=
,b=﹣1或a=![]() ,b=4.
,b=4.
【解析】
(1)从抛物线的顶点式就可以知道抛物线的顶点坐标,点C的纵坐标令x=0即可.
(2)求证两个角相等,可以证这两个角的三角函数相等.
(3)分情况讨论,利用全等三角形找到线段之间的数量关系,表示点坐标,代入解析式即可求出a、b.
(1)∵抛物线的解析式为y=a(x﹣4)2﹣16,
∴抛物线的顶点D的坐标为(4,﹣16),
当x=0时,y=16a﹣16,
∴点C的纵坐标为16a﹣16.
(2)∵D(4,﹣16),
∴OH=4.
∵AF=AH=OH,EH=HF,
∴F(12,0),A(8,0),E(﹣4,0),
将点F代入抛物线解析式得:
∴0=a(12﹣4)2﹣16,a![]() ,
,
将点A代入直线解析式得:![]() 8+b=0,b
8+b=0,b![]() ,
,
将a代入点C的纵坐标得:∴16a﹣16=﹣12,
∴C(0,﹣12),OC=12,tan∠CEO![]() 3,tan∠OBA
3,tan∠OBA![]() 3,
3,
∴∠CEO=∠ABO.
(3)分三种情况讨论:
①如图所示.
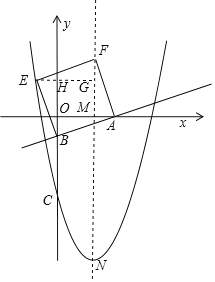
∵y![]() x+b,当x=0时,y=b,
x+b,当x=0时,y=b,
∴B(0,b),
过点E作EG垂直于NF,设对称轴与x轴的交点为M,BG与y轴的交点为点H.
∵四边形EFAB为正方形,可知△EFG≌△ABO(AAS),△FMA≌△ABO(AAS),∴OB=AM=FG=﹣b.
∵抛物线的对称轴为直线x=4,
∴OA=FM=EG=4﹣b,
∴A(4﹣b,0),E(b,4),
将点A代入直线解析式得:0![]() (4﹣b)+b,解得:b=﹣2,
(4﹣b)+b,解得:b=﹣2,
∴E(﹣2,4),
∴4=a(﹣2﹣4)2﹣16,
解得:a![]() .故a
.故a![]() ,b=﹣2.
,b=﹣2.
②如图所示.
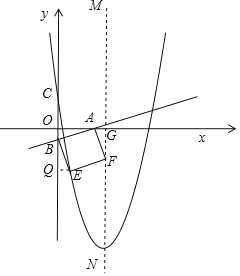
△OBA≌△AFG(AAS),△OBA≌△BEQ(AAS),
∴OB=EQ=AG=﹣b,
∴OA=FG=BQ=4+b,
∴A(4+b,0),E(﹣b,﹣4),
将点A代入直线解析式得:0![]() (4+b)+b,解得:b=﹣1,
(4+b)+b,解得:b=﹣1,
∴E(1,﹣4),将点E(1,﹣4)代入抛物线解析式得:﹣4=a(1﹣4)2﹣16,
解得:a![]() .故a
.故a![]() ,b=﹣1.
,b=﹣1.
③如图所示.
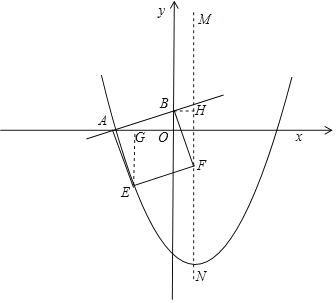
△ABO≌△EAG(AAS),△ABO≌△FBH(AAS),
∴OB=BH=AG=4,
∴b=4,
∴OA=12,EG=12,
∴E(﹣8,﹣12),
代入抛物线解析式得:﹣12=a(﹣8﹣4)2﹣16,解得:a![]() .
.
故a![]() ,b=4.
,b=4.
综上所述:a![]() ,b=﹣2或a
,b=﹣2或a![]() ,b=﹣1或a
,b=﹣1或a![]() ,b=4.
,b=4.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
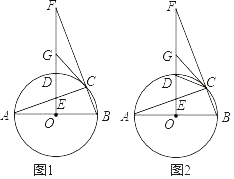
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
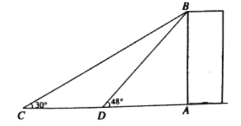
【题目】如图,某校数学兴趣小组要测量大楼AB的高度,他们在点C处测得楼顶B的仰角为30°,再往大楼AB方向前进至点D处测得楼顶B的仰角为48°,CD=96m,其中点A、D、C在同一直线上.求AD的长和大楼AB的高度(结果精确到1m)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73
≈1.73
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查作业:了解你所住小区家庭3月份用气量情况
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
(1)小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.
(2)在表3中,调查的15个家庭中使用气量的中位数是 m3,众数是 m3.
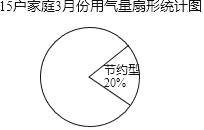
(3)小东将表2中的数据按用气量x(m3)大小分为三类.
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)小芸算出表3中3月份平均每人的用气量为6m3,请估计该小区3月份的总用气量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于![]() CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.
CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机场为了方便旅客换乘,计划在一、二层之间安装电梯,截面设计图如图所示,已知两层AD与BC平行,层高AB为8米,A、D间水平距离为5米,∠ACB=21.5°,
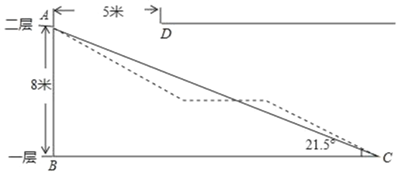
(1)通过计算说明身高2.4米的人在竖直站立的情况下,搭乘电梯在D处会不会碰到头部;
(2)若采用中段加平台设计(如图虚线所示),已知平台MN∥BC,且AM段和NC段的坡度均为1:2(坡度是指坡面的铅直高度与水平宽度的比),求平台MN的长度.
(参考数据:sin21.5°=![]() ,cos21.5°=
,cos21.5°=![]() ,tan21.5°=
,tan21.5°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com