
����Ŀ��ij����Ϊ�˷����ÿͻ��ˣ��ƻ���һ������֮�䰲װ���ݣ��������ͼ��ͼ��ʾ����֪����AD��BCƽ�У����ABΪ8�ף�A��D��ˮƽ����Ϊ5�ף���ACB��21.5����
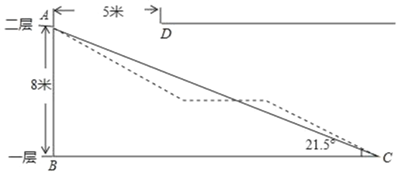
��1��ͨ������˵������2.4��������ֱվ��������£���˵�����D���������ͷ����
��2���������жμ�ƽ̨��ƣ���ͼ������ʾ������֪ƽ̨MN��BC����AM�κ�NC�ε��¶Ⱦ�Ϊ1��2���¶���ָ�����Ǧֱ�߶���ˮƽ���ȵıȣ�����ƽ̨MN�ij��ȣ�
���ο����ݣ�sin21.5����![]() ��cos21.5����
��cos21.5����![]() ��tan21.5����
��tan21.5����![]() ��
��
���𰸡���1��������ͷ������2��MN��4�ף�
��������
��1���ȹ���D��GD��AD����AC�ڵ�G�����ݡ�ACB=21.5�㣬AD��CB���ó���DAG=21.5�㣬�ٸ������ж������DG�ij���Ȼ�����˵����߽��бȽϣ����ɵó��𰸣�
��2������AB�ij����CB���ٹ���M��ME��AB������Ϊ��E������N��NF��CD������Ϊ��F����FN=x����AE=8��x������AM�κ�NC�ε��¶�i=1��2�����EM��CF�ij���������MN=BC����EM+CF������������𰸣�
��1����GD��AD����AC�ڵ�G��
�ߡ�ACB=21.5�㣬AD��BC�����DAG=21.5�㣬��DG=tan21.5���5=0.4��5=2��2.4���������ͷ����
��2����AB=8����CB=AB��tan21.5��=8��![]() =20��
=20��
����M��ME��AB��������E������N��NF��CD��������F����FN=x����AE=8��x��
��AM�κ�NC�ε��¶�i=1��2����EM=2��8��x��=16��2x��CF=2x����EM+CF=16��2x+2x=16����MN=BC����EM+CF��=20��16=4���ף���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������8��00��ij������������˴�ͳ�ǰ�����麣��¡�����Σ����麣��¡�������������100ǧ�ף�������ij�������飬��8��30�Ӹ��������Լ�С���Դ��1.5�����ٶ��ϣ��ϴ�ͺ����ǰ�У�����ȸ���������ǰ20���ӵ������麣��¡����
��1�������С����ƽ���ٶȸ��Ƕ��٣�
��2��������ij�ϴ�͵ĵص㵽���麣��¡����·���ж�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
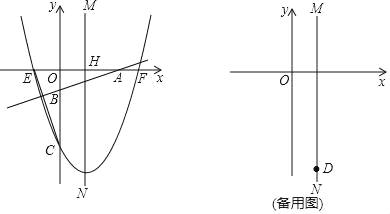
����Ŀ����ͼ��ֱ������ϵ�У�������y��a��x��4��2��16��a��0����x���ڵ�E��F��E��F����ߣ�����y���ڵ�C���Գ���MN��x���ڵ�H��ֱ��y��![]() x+b�ֱ�x��y���ڵ�A��B��
x+b�ֱ�x��y���ڵ�A��B��
��1��д���������߶���D�����꼰��C�������꣨�ú�a�Ĵ���ʽ��ʾ����
��2����AF��AH��OH����֤����CEO����ABO��
��3����b����4ʱ����ABΪ���������Σ�ʹ�����ε�������������һ�������������ϣ�һ�����������ߵĶԳ����ϣ�����������������a����Ӧb��ֵ����ֱ��д���𰸼��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
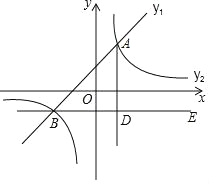
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y1��ax+b��ͼ���뷴��������y2��![]() ��ͼ���ڵ�A(1��2)��B(��2��m)��
��ͼ���ڵ�A(1��2)��B(��2��m)��
(1)��һ�κ����ͷ����������ı���ʽ��
(2)��ֱ��д��y1��y2ʱx��ȡֵ��Χ��
(3)����B��BE��x�ᣬAD��BE�ڵ�D����C��ֱ��BE��һ�㣬����DAC��30�������C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǰ뾶Ϊ1�ġ�O���������ߣ���A��B�ֱ�Ϊ�е㣬��APB��60����OP����AB���ڵ�C�����O���ڵ�D����Ӱ���ֵ������_____���������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
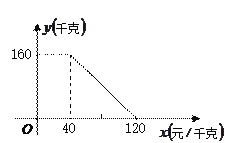
����Ŀ��ij�̵���40Ԫ/ǧ�˵Ľ��۹���һ����Ҷ�������鷢�֣���һ��ʱ���ڣ�������![]() (ǧ��)�����ۼ�
(ǧ��)�����ۼ�![]() (Ԫ/ǧ��)��һ�κ�����ϵ����ͼ����ͼ��ʾ.
(Ԫ/ǧ��)��һ�κ�����ϵ����ͼ����ͼ��ʾ.
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ(����д���Ա���
֮��ĺ�����ϵʽ(����д���Ա���![]() ��ȡֵ��Χ)��
��ȡֵ��Χ)��
��2�������̵�����������Ҷ�ijɱ�������2800Ԫ��������������ۼ�Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
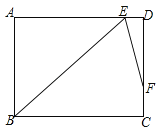
����Ŀ���ھ���ABCD�У���B�Ľ�ƽ����BE��AD���ڵ�E����BED�Ľ�ƽ����EF��DC���ڵ�F����AB=9��DF=2FC����BC=____��������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC����A(6,0)��C��0,4����ֱ��![]() �ֱ�BA��OA�ڵ�D��E����DΪBA�е㡣
�ֱ�BA��OA�ڵ�D��E����DΪBA�е㡣
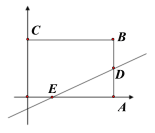
��1����k��ֵ����ʱ��EAD�������
��2��������������Ͷ���ڣ���������ڡ�EAD�ڵĸ��ʡ�����Ͷ�ڱ߿�������Ͷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�AD��y�ᣬ����Ϊ��E������A�ڵڶ����ޣ�����B��y����������ϣ�����������y��![]() (k��0��x��0)��ͼ������C��D������C�ĺ�����Ϊ5��BE��3DE����k��ֵΪ______��
(k��0��x��0)��ͼ������C��D������C�ĺ�����Ϊ5��BE��3DE����k��ֵΪ______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com