
分析 先化简各数,然后在数轴上表示出各数,再按照数轴的特点从左到右用“<”把各数连接起来即可.
解答 解:-(-2)=2,-|-$\frac{1}{2}$|=-$\frac{1}{2}$,+(-$\frac{2}{3}$)=-$\frac{2}{3}$,-1,|-$\frac{2}{3}$|=$\frac{2}{3}$,-[-(-3)]=-3.
数轴上表示如下: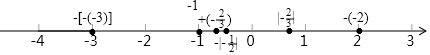
-[-(-3)]<-1<+(-$\frac{2}{3}$)<-|-$\frac{1}{2}$|<|-$\frac{2}{3}$|<-(-2).
点评 本题考查的是有理数的大小比较,数轴,解答此题的关键是熟知数轴上右边的数总大于左边的数.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:解答题
 如图,已知△ABC是边长为12cm的等边三角形,动点P,Q同时从AB两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是2cm/s,点Q运动的速度是4cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
如图,已知△ABC是边长为12cm的等边三角形,动点P,Q同时从AB两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是2cm/s,点Q运动的速度是4cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
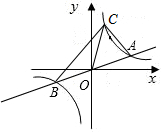 如图,反比例函数y=$\frac{3}{x}$的图象与直线y=ax(a≠0)交于A,B两点,点A的横坐标为3,
如图,反比例函数y=$\frac{3}{x}$的图象与直线y=ax(a≠0)交于A,B两点,点A的横坐标为3,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知OP平分∠MON,A是射线OM上一点.按要求完成下列各小题.(保留作图痕迹,不要求写作法)
如图,已知OP平分∠MON,A是射线OM上一点.按要求完成下列各小题.(保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
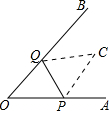 已知∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2,将∠O沿PQ折叠,点O落在平面内的点C处
已知∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2,将∠O沿PQ折叠,点O落在平面内的点C处查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com