
 如图,已知OP平分∠MON,A是射线OM上一点.按要求完成下列各小题.(保留作图痕迹,不要求写作法)
如图,已知OP平分∠MON,A是射线OM上一点.按要求完成下列各小题.(保留作图痕迹,不要求写作法) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着科技的发展,无人机的应用越来越广泛,2016年7月14日多家记者用无人飞机航拍湖北第二大湖炸堤泄洪画面.如图,无人飞机从A处水平飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
随着科技的发展,无人机的应用越来越广泛,2016年7月14日多家记者用无人飞机航拍湖北第二大湖炸堤泄洪画面.如图,无人飞机从A处水平飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
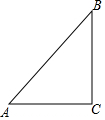 如图,在Rt△ABC中,∠C=90°,∠BAC=45°.
如图,在Rt△ABC中,∠C=90°,∠BAC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com