Question

【题目】如图1，对于平面上小于等于90°的∠MON，我们给出如下定义：若点P在∠MON的内部或边上，作PE⊥OM于点E，PF⊥ON于点F，则将PE+PF称为点P与∠MON的“点角距”，记作d（∠MON，P）．如图2，在平面直角坐标系xOy中，x、y正半轴所组成的角为∠xOy．

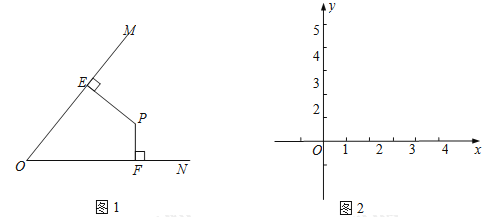
（1）已知点A（5，0）、点B（3，2），则d（∠xOy，A）= ，d（∠xOy，B）= ．

（2）若点P为∠xOy内部或边上的动点，且满足d（∠xOy，P）=5，画出点P运动所形成的图形．

（3）如图3与图4，在平面直角坐标系xOy中，射线OT的函数关系式为y=x（x≥0）．

①在图3中，点C的坐标为（4，1），试求d（∠xOT，C）的值；

②在图4中，抛物线y=-x2+2x+经过A（5，0）与点D（3，4）两点，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求当d（∠xOT，Q）取最大值时点Q 的坐标．

Answer 1

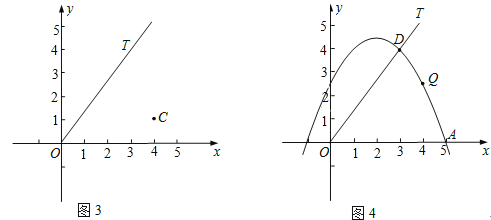
【答案】（1）5，5；（2）点P运动所形成的图形是线段y=5-x（0≤x≤5）．（3）；点Q的坐标为（4，）．

【解析】

试题分析：（1）首先根据点A（5，0）到x轴的距离是0，到y轴的距离是5，可得d（∠xOy，A）=0+5=5；然后根据点B（3，2）到x轴的距离是2，到y轴的距离是3，求出d（∠xOy，B）的值是多少即可．

（2）首先设点P的坐标是（x，y），然后根据d（∠xOy，P）=5，可得x+y=5，据此求出点P运动所形成的图形即可．

（3）①首先作CE⊥OT于点E，CF⊥x轴于点F，延长FC交OT于点H，则CF=1，然后设直线OT对应的函

数关系式为y=x（x≥0），求出点H的坐标为H（4，），进而求出CH，OH的值各是多少；最后根据相似三角形判定的方法，判断出△HEC∽△HFO，即可判断出，据此求出EC的值，即可求出d（∠xOT，C）的值是多少．

②首先作QG⊥OT于点G，QH⊥x轴于点H，交OT于点K，设点Q的坐标为（m，n），其中3≤m≤5，则n

=-m2+2m+，然后判断出点K的坐标，以及HK，OK的大小，再判断出Rt△QGK∽Rt△OHK，即可判断出，据此求出QG=；最后求出d（∠xOT，Q）的值，根据二次函数最值的求法，求出当d（∠xOT，Q）取最大值时点Q 的坐标即可．

试题解析：（1）∵点A（5，0）到x轴的距离是0，到y轴的距离是5，

∴d（∠xOy，A）=0+5=5，

∵点B（3，2）到x轴的距离是2，到y轴的距离是3，

∴d（∠xOy，B）=2+3=5．

综上，可得d（∠xOy，A）=5，d（∠xOy，B）=5．

（2）设点P的坐标是（x，y），

∵d（∠xOy，P）=5，

∴x+y=5，

∴点P运动所形成的图形是线段y=5-x（0≤x≤5）．

（3）①如图3，作CE⊥OT于点E，CF⊥x轴于点F，延长FC交OT于点H，则CF=1，

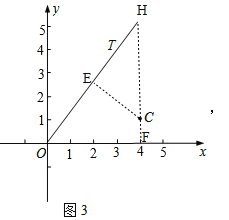
∵直线OT对应的函数关系式为y=x（x≥0），

∴点H的坐标为H（4，），

∴CH=1=，OH=

∵CE⊥OT，

∴∠OHF+∠HCE=90°，

又∵∠OHF+∠HOF=90°，

∴∠HCE=∠HOF，

在△HEC和△HFO中，

∴△HEC∽△HFO，

∴，

即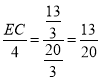

∴EC=，

∴d（∠xOT，C）=+1=

②如图4，作QG⊥OT于点G，QH⊥x轴于点H，交OT于点K，

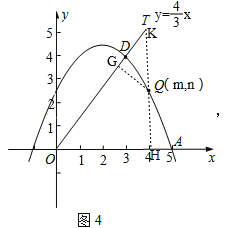
设点Q的坐标为（m，n），其中3≤m≤5，

则n=-m2+2m+，

∴点K的坐标为（m，m），QK=mn，

∴HK=m，OK=m．

∵Rt△QGK∽Rt△OHK，

∴，

∴QG=，

∴d（∠xOT，Q）=QG+QH

=+n

=m+n

=m+（-m2+2m+）

=-m2+m+1

=（m-4）2+

∵3≤m≤5，

∴当m=4时，d（∠AOB，Q）取得最大值．

此时，点Q的坐标为（4，）．