
【题目】如图,数轴上两点![]() 分别表示有理数2和5,我们用
分别表示有理数2和5,我们用![]() 来表示
来表示![]() 两点之间的距离.
两点之间的距离.
![]()
(1)直接写出![]() 的值=______;
的值=______;
(2)若数轴上一点![]() 表示有理数m,则
表示有理数m,则![]() 的值是______;
的值是______;
(3)当代数式∣n +2∣+∣n 5∣的值取最小值时,写出表示n的点所在的位置;
(4)若点![]() 分别以每秒2个单位长度和每秒3个单位长度的速度同时向数轴负方向运动,求经过多少秒后,点
分别以每秒2个单位长度和每秒3个单位长度的速度同时向数轴负方向运动,求经过多少秒后,点![]() 到原点的距离是点
到原点的距离是点![]() 到原点的距离的2倍.
到原点的距离的2倍.
【答案】(1)7;(2)![]() ;(3)
;(3)![]() ;(4)1秒或3秒
;(4)1秒或3秒
【解析】
(1)根据两点间距离公式求解即可;
(2)根据两点间距离公式求解即可;
(3)根据n+2和n-5以及两点间距离公式,即可得出n的取值范围;
(4)设经过x秒后点A到原点的距离是点B到原点的距离的2倍,利用两点间距离公式分两种情况列出方程,求解即可.
解:(1)![]()
故答案为:7
(2)![]()
(3)n点位于线段AB上(包括A、B两点),即![]() 时有最小值7;
时有最小值7;
即:![]()
(4)设经过x秒后点A到原点的距离是点B到原点的距离的2倍,
第一种情况:2+2x=2(5-3x),解得:x=1
第二种情况:2+2x=2(3x-5),解得:x=3
答:经过1秒或3秒后点A到原点的距离是点B到原点的距离的2倍.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
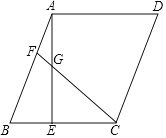
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解题过程,回答问题.
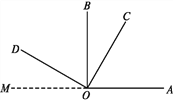
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对于平面上小于等于90°的∠MON,我们给出如下定义:若点P在∠MON的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON的“点角距”,记作d(∠MON,P).如图2,在平面直角坐标系xOy中,x、y正半轴所组成的角为∠xOy.
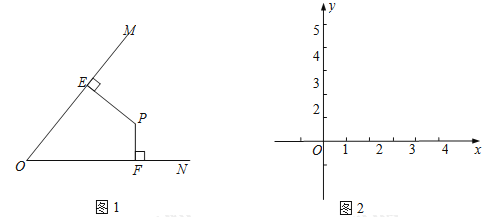
(1)已知点A(5,0)、点B(3,2),则d(∠xOy,A)= ,d(∠xOy,B)= .
(2)若点P为∠xOy内部或边上的动点,且满足d(∠xOy,P)=5,画出点P运动所形成的图形.
(3)如图3与图4,在平面直角坐标系xOy中,射线OT的函数关系式为y=![]() x(x≥0).
x(x≥0).
①在图3中,点C的坐标为(4,1),试求d(∠xOT,C)的值;
②在图4中,抛物线y=-![]() x2+2x+
x2+2x+![]() 经过A(5,0)与点D(3,4)两点,点Q是A,D两点之间的抛物线上的动点(点Q可与A,D两点重合),求当d(∠xOT,Q)取最大值时点Q 的坐标.
经过A(5,0)与点D(3,4)两点,点Q是A,D两点之间的抛物线上的动点(点Q可与A,D两点重合),求当d(∠xOT,Q)取最大值时点Q 的坐标.
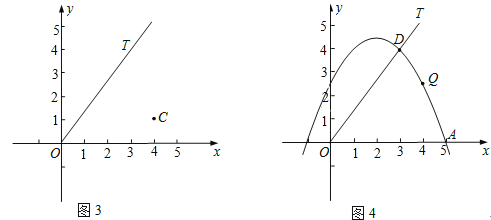
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
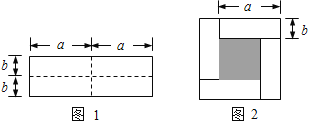
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = _____________;
= _____________;
(方法2)![]() =______________;
=______________;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() (如图),点
(如图),点![]() 分别在边
分别在边![]() 上,且四边形
上,且四边形![]() 是菱形
是菱形
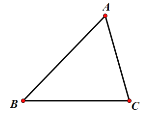
(1)请使用直尺与圆规,分别确定点![]() 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);
(2)如果![]() ,点
,点![]() 在边
在边![]() 上,且满足
上,且满足![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)当![]() 时,求
时,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
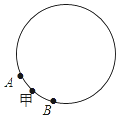
【题目】如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B的坐标分别为(-2,0),(![]() ,0),AD=2,∠DAB=60°点P从点A出发沿A→D→C运动到点C,连接PO.当PO=OB时,点P的坐标为___.
,0),AD=2,∠DAB=60°点P从点A出发沿A→D→C运动到点C,连接PO.当PO=OB时,点P的坐标为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com