
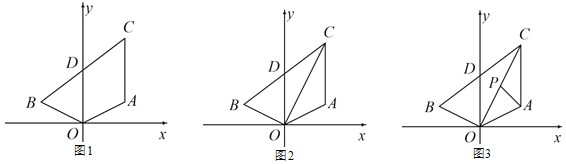
【题目】如图 1,点 A(2,1),点 A 与点 B 关于 y 轴对称,AC∥y 轴,且 AC=3,连接 BC 交 y 轴于点 D.
(1)点 B 的坐标为_____,点 C 的坐标为_____;
(2)如图 2,连接 OC,OC 平分∠ACB,求证:OB⊥OC;
(3)如图 3,在(2)的条件下,点 P 为 OC 上一点,且∠PAC=45°,求点 P 的坐标.
【答案】(1)(-2,1) (2,4);(2)见解析;(3)P(1,2)
【解析】
(1)由轴对称可得B、C点坐标;
(2)由OC 平分∠ACB,可得∠1=∠2,又∠3=∠2,可得CD=DO,CE⊥y 轴于点 E,连接 AB 交 y 轴于点 F,可证的△CDE≌△BDF(AAS),可得CD=BD,BD=CD=OD,∠DBO=∠DOB,可得OB⊥OC;
(3)连接 BP,作 PQ⊥x 轴于点 Q,由点 A,点 B 关于 y 轴对称 可得∠BAC =90,∠PAC =45,PA 平分∠CAB,可证的OB=OP,可得△BOF≌△POQ(AAS).可得PQ=BF=2,OQ=OF=1,P(1,2).
(1)B(-2,1),C(2,4).
(2)∵OC 平分∠ACB,
∴∠1=∠2,
∵AC∥y 轴,
∴∠3=∠2,
∴∠1=∠3,
∴CD=DO.
作 CE⊥y 轴于点 E,连接 AB 交 y 轴于点 F,
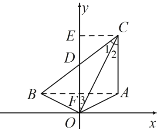
∵点 A,点 B 关于 y 轴对称,
∴BF⊥y 轴,
∴∠CED=∠BFD,
∵B(-2,1),C(2,4),
∴CE=BF=2,
在△CDE 和△BDF 中,
CED BFDCDE BDF,CE BF,
∴△CDE≌△BDF(AAS).
∴CD=BD,
∴BD=CD=OD,
∴∠DBO=∠DOB,
∵∠1+∠3+∠DBO+∠DOB=180°,
∴∠3+∠DOB=90°,
∴OB⊥OC;
(3)连接 BP,作 PQ⊥x 轴于点 Q,
∵点 A,点 B 关于 y 轴对称,
∴AB⊥y 轴,
∴∠BAC =90,
∵∠PAC =45,
∴PA 平分∠CAB,
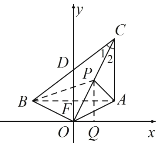
∵OC 平分∠ACB,
∴BP 平分∠ABC.
∴∠BPC=135°,
∴∠BPO=45°.
∵∠BOP=90°,
∴OB=OP,
在△BOF 和△POQ 中,
BFO PQO,BOF POQ,OB OP,
∴△BOF≌△POQ(AAS).
∴PQ=BF=2,OQ=OF=1,
∴P(1,2).


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
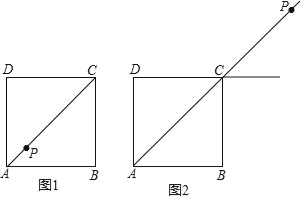
【题目】在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP.
(1)当点P在线段AC上时,如图1.
①依题意补全图1;
②若EQ=BP,则∠PBE的度数为 ,并证明;
(2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1,请写出求BE长的思路.(可以不写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地在山区修建高速公路时需挖通一条隧道,为估计这条隧道的长度需测出这座山A、B间的距离,结合所学知识或方法,设计测量方案你能给出什么好的方法吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F. 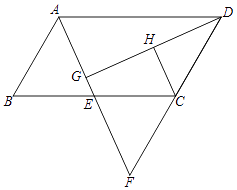
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系, 并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=mx2+(m2﹣m)x﹣2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.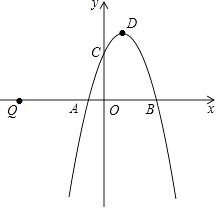
(1)求二次函数的表达式及A、B的坐标;
(2)若P(0,t)(t<﹣1)是y轴上一点,Q(﹣5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
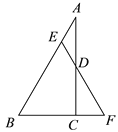
【题目】如图,在 Rt△ABC 中,∠A=30°,∠ACB=90°,点 D 为 AC 中点, 点 E 为 AB 边上一动点,AE=DE,延长 ED 交 BC 的延长线于点 F.
(1)求证:△BEF 是等边三角形;
(2)若 AB=12,求 DE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,请仔细观察并找出规律,解答下列问题:

(1)按照此规律,摆第n个图时,需用火柴棒的根数是多少?
(2)求摆第50个图时所需用的火柴棒的根数;
(3)按此规律用1202根火柴棒摆出第n个图形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com