
【题目】如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F. 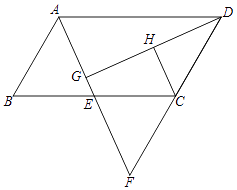
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系, 并说明理由.
【答案】
(1)解:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠ECF
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
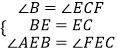
∴△ABE≌△FCE.
(2)解:结论:CH⊥DG.理由如下:
∵△ABE≌△FCE,
∴AB=CF,
∵AB=CD,
∴DC=CF,
∵H为DG的中点,
∴CH∥FG
∵DG⊥AE,
∴CH⊥DG.
【解析】(1)根据平行四边形的性质,利用ASA即可证明.(2)结论:CH⊥DG.利用三角形中位线定理,证明CH∥AF即可解决问题.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(3,1),将矩形沿对角线BO翻折,C点落在D点的位置,且BD交x轴于点E.那么点D的坐标为 . 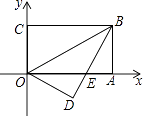
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
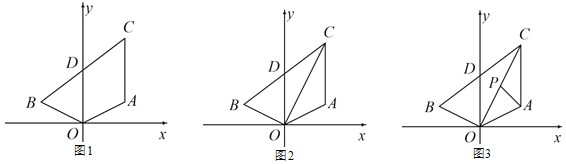
【题目】如图 1,点 A(2,1),点 A 与点 B 关于 y 轴对称,AC∥y 轴,且 AC=3,连接 BC 交 y 轴于点 D.
(1)点 B 的坐标为_____,点 C 的坐标为_____;
(2)如图 2,连接 OC,OC 平分∠ACB,求证:OB⊥OC;
(3)如图 3,在(2)的条件下,点 P 为 OC 上一点,且∠PAC=45°,求点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员把全班45名同学的体育锻炼时间,并绘制了如图所示的折线统计图,则全班45名同学一周的体育锻炼总时间的众数和中位数分别是( ) 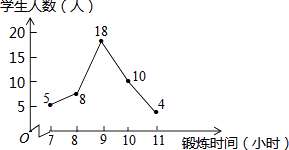
A.9,9
B.9,10
C.18,9
D.18,18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂去年的总产值比总支出多500万元,而今年计划的总产值比总支出多950万元.已知今年计划总产值比去年增加15%,而今年计划总支出比去年减少10%.求今年计划的总产值和总支出各为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示,直线l过点M(3,0)且平行于y轴.
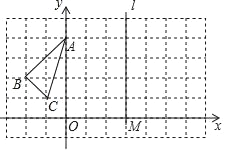
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求P1P2的长.(用含a的代数式表示)
(3)通过计算加以判断,PP2的长会不会随点P位置的变化而变化.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com