
【题目】已知反比例函数的图像经过点(2,-3).
(1)求这个函数的表达式.
(2)点(-1,6),(3,2)是否在这个函数的图像上?
(3)这个函数的图像位于哪些象限?函数值y随自变量![]() 的增大如何变化?
的增大如何变化?
【答案】(1)y=-![]() ;(2)(-1,6)在函数图像上,(3,2)不在函数图像上;(3)二、四象限,在每个象限内,y随x的增大而增大.
;(2)(-1,6)在函数图像上,(3,2)不在函数图像上;(3)二、四象限,在每个象限内,y随x的增大而增大.
【解析】
(1)根据待定系数法求得即可;
(2)根据图象上点的坐标特征,把点(﹣1,6),(3,2)代入解析式即可判断;
(3)根据反比例函数的性质即可得到结论.
(1)设反比例函数的解析式为y![]() (k≠0).
(k≠0).
∵反比例函数的图象经过点(2,﹣3),
∴k=2×(﹣3)=﹣6,
∴反比例函数的表达式y![]() ;
;
(2)把x=﹣1代入y![]() 得:y=6,
得:y=6,
把x=3代入y![]() 得:y=﹣2≠2,
得:y=﹣2≠2,
∴点(﹣1,6)在函数图象上,点(3,2)不在函数图象上.
(3)∵k=﹣6<0,
∴双曲线在二、四象限,在每个象限内y随x的增大而增大.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问题:
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的名称;
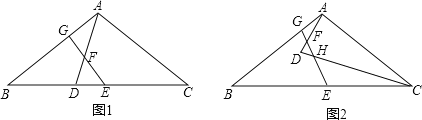
(2)如图1,在△ABC中,AB=AC,点D在BC上,且CD=CA,点E、F分别为BC、AD的中点,连接EF并延长交AB于点G.求证:四边形AGEC是等邻角四边形;
(3)如图2,若点D在△ABC的内部,(2)中的其他条件不变,EF与CD交于点H,图中是否存在等邻角四边形,若存在,指出是哪个四边形,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一元二次方程x2+2x﹣3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
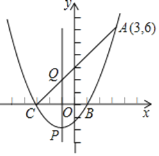
(1)求此二次函数的解析式;
(2)写出不等式ax2+bx+c≥0的解集;
(3)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标;
(4)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件成本40元,出于营销考虑,要求每件售价不得低于40元,但物价部门要求每件售价不得高于60元.据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每涨1元,每天就少售出2件,设单价上涨![]() 元
元![]() .
.
(1)求当![]() 为多少时每天的利润是1350元?
为多少时每天的利润是1350元?
(2)设每天的销售利润为![]() ,求销售单价为多少元时,每天利润最大?最大利润是多少?
,求销售单价为多少元时,每天利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
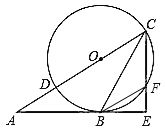
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
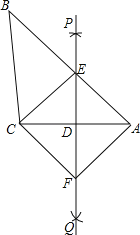
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若ED=6,AE=10,则菱形AECF的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于![]() 左右,求n的值;
左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com