
【题目】阅读下面材料,解答后面的问题.
解方程:![]() -
-![]() =0.
=0.
解:设y=![]() ,则原方程可化为y-
,则原方程可化为y-![]() =0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.
=0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.
经检验,y1=2,y2=-2都是方程y-![]() =0的解.
=0的解.
当y=2时,![]() =2,解得x=-1;当y=-2时,
=2,解得x=-1;当y=-2时,![]() =-2,解得x=
=-2,解得x=![]() .
.
经检验,x1=-1,x2=![]() 都是原分式方程的解.所以原分式方程的解为x1=-1,x2=
都是原分式方程的解.所以原分式方程的解为x1=-1,x2=![]() .
.
上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程![]() -
-![]() =0中,设y=
=0中,设y=![]() ,则原方程可化为________________;
,则原方程可化为________________;
(2)若在方程![]() -
-![]() =0中,设y=
=0中,设y=![]() ,则原方程可化为________________;
,则原方程可化为________________;
(3)模仿上述换元法解方程:![]() -
-![]() -1=0.
-1=0.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)x=-
;(3)x=-![]() .
.
【解析】
(1)将所设的y代入原方程即可;
(2)将所设的y代入原方程即可;
(3)利用换元法解分式方程,设y=![]() ,将原方程化为y
,将原方程化为y![]() =0,求出y的值并检验是否为原方程的解,然后求解x的值即可.
=0,求出y的值并检验是否为原方程的解,然后求解x的值即可.
(1)将y=![]() 代入原方程,则原方程化为
代入原方程,则原方程化为![]()
![]() =0;
=0;
(2)将y=![]() 代入方程,则原方程可化为y
代入方程,则原方程可化为y![]() =0;
=0;
(3)原方程可化为![]() -
-![]() =0,设y=
=0,设y=![]() ,则原方程可化为y-
,则原方程可化为y-![]() =0,
=0,
方程两边同时乘y,得y2-1=0,解得y1=1,y2=-1,
经检验,y1=1,y2=-1都是方程y-![]() =0的解;
=0的解;
当y=1时,![]() =1,该方程无解;当y=-1时,
=1,该方程无解;当y=-1时,![]() =-1,解得x=-
=-1,解得x=-![]() ,
,
经检验,x=-![]() 是原分式方程的解,
是原分式方程的解,
所以原分式方程的解为x=-![]() .
.


科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合中.
-![]() ,π,3.14,-
,π,3.14,-![]() ,0,-5.123 45…,
,0,-5.123 45…,![]() ,-
,-![]() .
.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )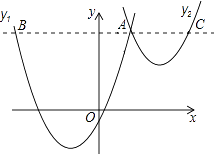
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小学,我们已经初步了解到,长方形的对边平行且相等,每个角都是90°.如图,长方形ABCD中,AD=9cm,AB=4cm,E为边AD上一动点,从点D出发,以1cm/s向终点A运动,同时动点P从点B出发,以acm/s向终点C运动,运动的时间为ts.
(1)当t=3时,
①求线段CE的长;
②当EP平分∠AEC时,求a的值;
(2)若a=1,且△CEP是以CE为腰的等腰三角形,求t的值;
(3)连接DP,直接写出点C与点E关于DP对称时的a与t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G. 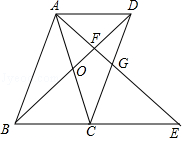
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD,请使用无刻度直尺画图.
(1)在图1中画出一个与梯形ABCD面积相等,且以CD为边的三角形;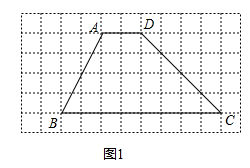
(2)图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形.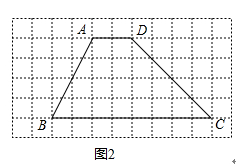
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交 ![]() 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( ) 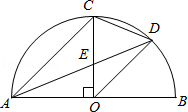
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 ![]() 的坐标为
的坐标为![]() ,以 A 为顶点的
,以 A 为顶点的![]() 的两边始终与
的两边始终与 ![]() 轴交于
轴交于 ![]() 、
、![]() 两点(
两点(![]() 在
在 ![]() 左面),且
左面),且![]() .
.
(1)如图,连接![]() ,当
,当 ![]() 时,试说明:
时,试说明:![]() .
.

(2)过点 ![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,当
,当![]() 时,将
时,将![]() 沿
沿![]() 所在直线翻折,翻折后边
所在直线翻折,翻折后边![]() 交
交 ![]() 轴于点
轴于点 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com