Question

【题目】在平面直角坐标系中，点 的坐标为，以 A 为顶点的的两边始终与 轴交于 、两点（在 左面），且．

（1）如图，连接，当 时，试说明：．

（2）过点 作轴，垂足为，当时，将沿所在直线翻折，翻折后边 交 轴于点 ，求点 的坐标.

Answer 1

【答案】(1)见解析；(2)M点坐标为（0,3)或M点坐标为(0，—6).

【解析】

试题(1)根据题目中角的度数，求出∠BAO=∠ABC=67.5°，利用等腰三角形的性质即可得出结论；

(2)根据题意，可知要分两种情况，即当点C在点D右侧时或当点C在点D左侧时，利用勾股定理即可得出M点坐标.

试题解析：

（1）∵AB=AC，∠BAC=45°，∴∠ABC=∠ACB= 67.5°.

过点A作AE⊥OB于E，则△AEO是等腰直角三角形，∠EAO=45°.

∵AB=AC，AE⊥OB，

∴∠BAE=∠BAC=22.5°.

∴∠BAO=67.5°=∠ABC

∴OA=OB，

（2）设OM=x.

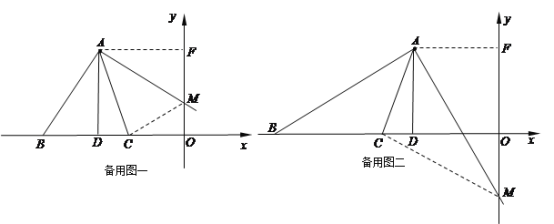
当点C在点D右侧时，连接CM，过点A作AF⊥y轴于点F，

由∠BAM=∠DAF=90°可知：∠BAD=∠MAF；

∵AD=AF=6，∠BDA=∠MFA=90°，

∴△BAD≌△MAF.

∴BD=FM=6—x.

∵AC=AC，∠BAC=∠MAC，

∴△BAC≌△MAC.

∴BC=CM=8—x.

在Rt△COM中，由勾股定理得：OC2+OM2=CM2，即，

解得：x=3，∴M点坐标为（0,3）.

当点C在点D左侧时，连接CM，过点A作AF⊥y轴于点F，

同理，△BAD≌△MAF，∴BD=FM=6+x.

同理，△BAC≌△MAC，∴BC=CM=4+x.

在Rt△COM中，由勾股定理得：OC2+OM2=CM2，即，

解得：x=6，∴M点坐标为（0，—6）