
����Ŀ������Ҫ��ش����⣺
��1����������⡿
��֪������ABCD�ı䳤Ϊ4����ADC=60�㣬��PEFΪ�ȱ������Σ�����P���D�غϣ���E�ڶԽ���AC��ʱ����ͼ1��ʾ������AE+AF��ֵ��
��2�������̽����
������������У�����ѵ�P��DA�����ƶ���ʹPD=1�������������䣨��ͼ2�������ܷ���AE+AF��ֵ�Ƕ��٣���ֱ��д����Ľ��ۣ�
��3������չǨ�ơ�
��ԭ�����У�����P���߶�DA���ӳ����ϣ���E��CA���ӳ�����ʱ����ͼ3������AP=m�����߶�AE��AF�ij���m��������������ϵ����˵�����ɣ�
���𰸡�
��1���⣺��ͼ1��
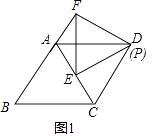 ��
��
���ı���ABCD�����Σ�
��PA=PC��
�ߡ�ADC=60�㣬
���ACD�ǵȱ������Σ�
��AC=AD=4��
�֡ߡ�PEFΪ�ȱ������Σ�
���ADC=��EPF=60�㣬
���APF=��CPE��
�ڡ�APF�͡�CPE�У�
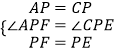
���APF�ա�CPE��
��CE=AF��
��AE+AF=AE+CE=AC=4��
��AE+AF��ֵ��4��
��2���⣺��ͼ2����G��AC�ϵ�һ�㣬������CG=PD=1��
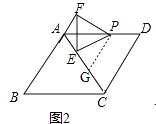 ��
��
��CG=PD��AC=AD��
��AG=AP��
�� ![]() ��
��
��GP��CD��
���GPA=��CDA=60�㣬
�֡�EPF=60�㣬
���APF=��GPE��
�ڡ�APF�͡�GPE�У�
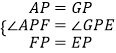
���APF�ա�GPE��
��GE=AF��
��AE+AF=AE+GE=AG=AC��CG=4��1=3��
��AE+AF��ֵ��3
��3���⣺��ͼ3����PH��CD��CE�ڵ�H��
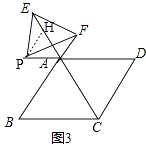 ��
��
�ɣ�1�����ɵá�ACD�ǵȱ������Σ�
��PH��CD��
���AHP�ס�ACD��
���AHP�ǵȱ������Σ�
��PA=PH����APH=��EPF=60�㣬
���FPA=��EPH��
�ڡ�APF�͡�HPE�У�
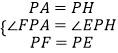
���APF�ա�HPE��
��AF=HE��
�֡�PA=AH��
��AE=PA+AF��
��AE��AF=m��
����������1�������жϳ���ACD�ǵȱ������Σ������жϳ�AC=AD=4��Ȼ�����ȫ���������ж��ķ������жϳ���APF�ա�CPE�������жϳ�CE=AF���ݴ����AE+AF��ֵ�Ƕ��ټ��ɣ���2������ȡAC�ϵĵ�G��ʹ��CG=PD=1���жϳ�GP��CD�������жϳ���APF=��GPE��Ȼ�����ȫ���������ж��ķ������жϳ���APF�ա�GPE�������жϳ�GE=AF���ݴ����AE+AF��ֵ�Ƕ��ټ��ɣ���3��������PH��CD��CE�ڵ�H���жϳ���AHP�ס�ACD�������жϳ���AHP�ǵȱ������Σ�Ȼ�����ȫ���������ж��ķ������жϳ���APF�ա�HPE�������жϳ�AF=HE���ٸ���PA=AH���ɵ�AE=PA+AF������AE��AF=m���ݴ˽�ɣ�
�����㾫����������Ĺؼ���������ȫ�������ε����ʵ����֪ʶ������ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ��Լ������ε����ʵ����⣬�˽����ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD��BEƽ�֡�ABC��DEƽ�֡�ADC����BAD��70������BCD��40�������BED�Ķ���Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��O��OE��AB��
��1������EOD=20��������AOC�Ķ�����
��2������AOC����BOC=1��2������EOD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������IJ�����㣺
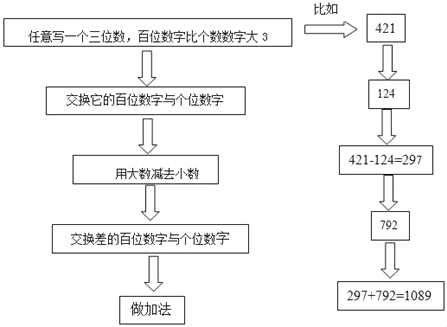
����дһ����λ������λ���ֱȸ������ִ�3������İ�λ�������λ�����ô�����ȥС���������İ�λ�������λ�������ӷ�
���⣺(1)�ò�ͬ����λ���������Σ��������1089��
(2)���ܽ������еĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() ��
��![]() ���ڲ�����
���ڲ�����![]() ���
���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ���
���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ����
����![]() ______��
______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������Ϊ��������ǣ� ��
�� ![]() ������ƽ������4��
������ƽ������4��
����ma2��na2 �� ��m��n��
�����˱��ε�һ���ڽǵĶ�����135�㣻
�ܶԽ����ഹֱƽ�ֵ��ı��������Σ�
��ƽ���ҵ�ֱ����ֱ���ң�
A.�٢ۢ�
B.�ڢۢ�
C.�٢ܢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ����һ�㣬����
����һ�㣬����![]() ����ʱ�н���
����ʱ�н���![]() �������������⣺
�������������⣺
��1����![]() ��
��![]() ���ϵ��е�ʱ��
���ϵ��е�ʱ��![]() �����
����� ![]() ��������>����<����=������
��������>����<����=������
��2����ͼ1����![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���ϵĵ㣬����
���ϵĵ㣬����![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ5��8��10����
������ֱ�Ϊ5��8��10����![]() ������� ��ֱ��д�����ۣ���
������� ��ֱ��д�����ۣ���
��3����ͼ2������![]() �ֱ���
�ֱ���![]() ��
��![]() ���ϵ��е㣬��
���ϵ��е㣬��![]() �����ı���
�����ı���![]() ����������������·���������
����������������·���������![]() ����
����![]() ��
��![]() ��ͬ����
��ͬ����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���������
���������![]() ��
��![]() �����з�����Ϊ��
�����з�����Ϊ��![]() �����
�����![]() ���ɵ��ı���
���ɵ��ı���![]() �����Ϊ20������������⣺
�����Ϊ20������������⣺
��ͼ3��![]() ��
��![]() �����ȷֵ㣬
�����ȷֵ㣬![]() ��
��![]() �����ȷֵ㣬
�����ȷֵ㣬![]() ��
��![]() ����
����![]() ����
����![]() ��������ı���
��������ı���![]() ���������˵�����ɣ�
���������˵�����ɣ�



ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��� ![]() ������Ϊ
������Ϊ![]() ���� A Ϊ�����
���� A Ϊ�����![]() ������ʼ����
������ʼ���� ![]() �ύ��
�ύ�� ![]() ��
��![]() ���㣨
���㣨![]() ��
�� ![]() ���棩����
���棩����![]() ��
��
��1����ͼ������![]() ����
���� ![]() ʱ����˵����
ʱ����˵����![]() ��
��

��2������ ![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ����
����![]() ʱ����
ʱ����![]() ��
��![]() ����ֱ�߷��ۣ����ۺ��
����ֱ�߷��ۣ����ۺ��![]() ��
�� ![]() ���ڵ�
���ڵ� ![]() �����
����� ![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����ֱ֪��![]() ����ֱ��
����ֱ��![]() ��ȡ
��ȡ![]() ���㣬
���㣬![]() Ϊֱ��
Ϊֱ��![]() �ϵ����㣬���۵�
�ϵ����㣬���۵�![]() �ƶ����κ�λ�ö��У�
�ƶ����κ�λ�ö��У�![]() ____________
____________![]() ������>������<������=����
������>������<������=����
��2����ͼ2����һ����������Ϸֱ�Ҫ��ֲ���հײ��֣���֥�飨��Ӱ���֣����������ֲ������ظ�Ϊһ��أ���ʹ�ֱ���ֲ����ֲ���������䣬����Ӧ����ô�Ľ��أ�д����Ʒ���������ͼ�л�����Ӧͼ�β��������ɣ�
��3����ͼ3����үү����үү��������γ����ı���![]() ���м������ֽ�С·��ͼ������
���м������ֽ�С·��ͼ������![]() �����������Ϊ��үү�ģ��ұ�����Ϊ��үү�ġ����������������֮���С·��Ϊֱ·���������йصļ���֪ʶ����Ҫ����Ƴ���·����������ͼ�л�����Ӧ��ͼ�Σ�˵������������ɡ������Ʒֽ�С·��ֱ·��ռ���������
�����������Ϊ��үү�ģ��ұ�����Ϊ��үү�ġ����������������֮���С·��Ϊֱ·���������йصļ���֪ʶ����Ҫ����Ƴ���·����������ͼ�л�����Ӧ��ͼ�Σ�˵������������ɡ������Ʒֽ�С·��ֱ·��ռ���������



�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com