
����Ŀ����1����ͼ1����ֱ֪��![]() ����ֱ��
����ֱ��![]() ��ȡ
��ȡ![]() ���㣬
���㣬![]() Ϊֱ��
Ϊֱ��![]() �ϵ����㣬���۵�
�ϵ����㣬���۵�![]() �ƶ����κ�λ�ö��У�
�ƶ����κ�λ�ö��У�![]() ____________
____________![]() ������>������<������=����
������>������<������=����
��2����ͼ2����һ����������Ϸֱ�Ҫ��ֲ���հײ��֣���֥�飨��Ӱ���֣����������ֲ������ظ�Ϊһ��أ���ʹ�ֱ���ֲ����ֲ���������䣬����Ӧ����ô�Ľ��أ�д����Ʒ���������ͼ�л�����Ӧͼ�β��������ɣ�
��3����ͼ3����үү����үү��������γ����ı���![]() ���м������ֽ�С·��ͼ������
���м������ֽ�С·��ͼ������![]() �����������Ϊ��үү�ģ��ұ�����Ϊ��үү�ġ����������������֮���С·��Ϊֱ·���������йصļ���֪ʶ����Ҫ����Ƴ���·����������ͼ�л�����Ӧ��ͼ�Σ�˵������������ɡ������Ʒֽ�С·��ֱ·��ռ���������
�����������Ϊ��үү�ģ��ұ�����Ϊ��үү�ġ����������������֮���С·��Ϊֱ·���������йصļ���֪ʶ����Ҫ����Ƴ���·����������ͼ�л�����Ӧ��ͼ�Σ�˵������������ɡ������Ʒֽ�С·��ֱ·��ռ���������



���𰸡���1��![]() ����2������������3��������
����2������������3��������
��������
��1������ƽ����ľ��봦����ȣ��������۵�![]() ��m���ƶ�����λ�ã�����
��m���ƶ�����λ�ã�����![]() ��
��![]() ͬ�ȸߣ�������ǵ������ȣ�
ͬ�ȸߣ�������ǵ������ȣ�
��2������ͬ�ȸߵ������ε������ȼ��������Ʒ�����
��3������![]() ����
����![]() ����
����![]() ��ƽ����
��ƽ����![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ��Ϊ����ֱ·��
��Ϊ����ֱ·��
��1����![]() ��
��![]() �й�ͬ�ı�AB��
�й�ͬ�ı�AB��
�֡�![]() ��
��
��![]() ��
��![]() �ĸ���ȣ���
�ĸ���ȣ���![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() =
=![]() ��
��
�ʴ�Ϊ��=��
��2������һ��
����![]() ����
����![]() ������������ֲ��
������������ֲ��![]() ������������ֲ֥�飬�������£�
������������ֲ֥�飬�������£�
������ABCD��,![]() ��
��
��![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��֪
��֪![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ��
��
�����Ʒ�������ֲ������ظ�Ϊһ��أ���ʹ�ֱ���ֲ����ֲ���������䣻
������
����![]() ����
����![]() ������������ֲ��
������������ֲ��![]() ������������ֲ֥�飬�������£�
������������ֲ֥�飬�������£�
������ABCD��,![]() ��
��
��![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��֪
��֪![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ��
��
�����Ʒ�������ֲ������ظ�Ϊһ��أ���ʹ�ֱ���ֲ����ֲ���������䣻

��3������һ
����![]() ����
����![]() ����
����![]() ��ƽ����
��ƽ����![]() ������
������![]() ��
��![]() ��Ϊ����ֱ·��
��Ϊ����ֱ·��
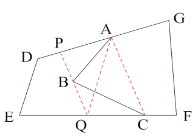
���ı���![]() ������ָ���үү���ı���
������ָ���үү���ı���![]() ������ָ���үү���������£�
������ָ���үү���������£�
��![]() ����
����![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ����
����![]() ��
��
��![]() ��
��
����![]() ��֪
��֪![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ��
��
��![]() ������·������
������·������
��������
����![]() ����
����![]() ����
����![]() ��ƽ����
��ƽ����![]() ������
������![]() ��
��![]() ��Ϊ����ֱ·��
��Ϊ����ֱ·��
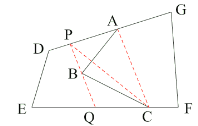
���ı���![]() ������ָ���үү���ı���
������ָ���үү���ı���![]() ������ָ���үү���������£�
������ָ���үү���������£�
��![]() ����
����![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ����
����![]() ��
��
��![]() ��
��
����![]() ��֪
��֪![]() ��
��![]() ͬ�ȸߣ�
ͬ�ȸߣ�
��![]() ��
��
��![]() ������·������
������·������


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ��ش����⣺
��1����������⡿
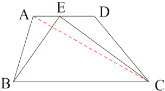
��֪������ABCD�ı䳤Ϊ4����ADC=60�㣬��PEFΪ�ȱ������Σ�����P���D�غϣ���E�ڶԽ���AC��ʱ����ͼ1��ʾ������AE+AF��ֵ��
��2�������̽����
������������У�����ѵ�P��DA�����ƶ���ʹPD=1�������������䣨��ͼ2�������ܷ���AE+AF��ֵ�Ƕ��٣���ֱ��д����Ľ��ۣ�
��3������չǨ�ơ�
��ԭ�����У�����P���߶�DA���ӳ����ϣ���E��CA���ӳ�����ʱ����ͼ3������AP=m�����߶�AE��AF�ij���m��������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ġ�ABC����ֱ�������ε��ǣ���
A. BC��1��AC��2��AB��![]()
B. BC��1��AC��2��AB��![]()
C. BC��AC��AB��3��4��5
D. ��A����B����C��3��4��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���̴������г���8000Ԫ�����˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ���ӣ�ҵĽ��۱�Сӣ�ҵĽ���ÿǧ�˶�20Ԫ.��ӣ���ۼ�Ϊÿǧ��40Ԫ��Сӣ���ۼ�Ϊÿǧ��16Ԫ.
(1)��ӣ�Һ�Сӣ�ҵĽ��۷ֱ���ÿǧ�˶���Ԫ?�������ˮ���̹��˶���ԪǮ?
(2)��ˮ���̵ڶ�������8000ԪǮ�������г������˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ����۲��䣬�������������Сӣ�������20%����Сӣ�ҵ��ۼ۲��䣬Ҫ���õڶ�����Ǯ�����ڵ�һ����Ǯ��90%����ӣ�ҵ��ۼ�����ӦΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��l1��y=��x+n����A����1��3����˫����C��y= ![]() ��x��0��������B��1��2������ֱ��l2��y=kx��2k+2������k��0���������F��
��x��0��������B��1��2������ֱ��l2��y=kx��2k+2������k��0���������F��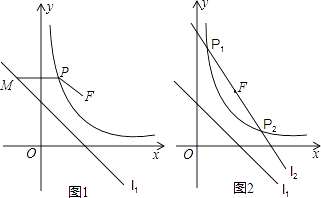
��1����ֱ��l1 �� ˫����C�Ľ���ʽ������F�����ꣻ
��2����˫����C��ȡһ��P��x��y������P��x���ƽ���߽�ֱ��l1��M������PF����֤��PF=PM��
��3������ֱ��l2��˫����C����P1 �� P2���㣬����OF��ֱ��l1�ڵ�E������P1E��P2E����֤��EFƽ�֡�P1EP2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǵ����߷ֱ�ƽ�У�������һ���DZ���һ���ǵ�2����30�������������ǵĶ����ֱ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ䣬ij�̳��ƻ������ס���������Ʒ����֪��������Ʒ2��������Ʒ3������270Ԫ����������Ʒ3��������Ʒ2������230Ԫ��
��1����ס���������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳���������Ʒ��ÿ��40Ԫ���ۣ�����Ʒ��ÿ��90Ԫ���ۣ�Ϊ�����г������蹺���ס���������Ʒ��100�����Ҽ�����Ʒ������������������Ʒ������4������������������Ľ���������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���ACB=90����DΪBC���е㣬DE��AB������ΪE������B��BF��AC��DE���ӳ����ڵ�F������CF��

��1����֤��AD��CF��
��2������AF�����ж���ACF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ��������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x+40 | 90 |
ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ��
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com