
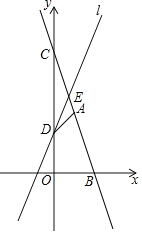
【题目】如图,过点A(1,3)的一次函数y=kx+6(k≠0)的图象分别与x轴,y轴相交于B,C两点.
(1)求k的值;
(2)直线l与y轴相交于点D(0,2),与线段BC相交于点E.
(i)若直线l把△BOC分成面积比为1:2的两部分,求直线l的函数表达式;
(ⅱ)连接AD,若△ADE是以AE为腰的等腰三角形,求满足条件的点E的坐标.
【答案】(1)-3;(2)(i)y=±x+2;(ⅱ)点E的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)将点A的坐标代入一次函数y=kx+6中,即可解得k的值;
(2)(i)先求出△BCO的面积,根据直线l把△BOC分成面积比为1:2的两部得出△CDE的面积,根据三角形面积公式得出E的横坐标,将横坐标代入y=kx+6即可得到E的坐标,点E的坐标代入直线l表达式,即可求出直线l表达式;
(ⅱ)设点E(m,﹣3m+6),根据两点间的距离公式列出方程,解得点E的坐标.
(1)将点A的坐标代入一次函数y=kx+6并解得:
k=﹣3;
(2)一次函数y=﹣3x+6分别与x轴,y轴相交于B,C两点,
则点B、C的坐标分别为:(2,0)、(0,6);
(i)S△BCO=![]() OB×CO=
OB×CO=![]() 2×6=6,
2×6=6,
直线l把△BOC分成面积比为1:2的两部分,
则S△CDE=2或4,
而S△CDE=![]() ×CD×
×CD×![]() =
=![]() 4×
4×![]() =2或4,
=2或4,
则![]() =1或2,
=1或2,
故点E(1,3)或(2,0),
将点E的坐标代入直线l表达式并解得:
直线l的表达式为:y=±x+2;
(ⅱ)设点E(m,﹣3m+6),而点A、D的坐标分别为:(1,3)、(0,2),
则AE2=(m﹣1)2+(3﹣3m)2,AD2=2,ED2=m2+(4﹣3m)2,
当AE=AD时,(m﹣1)2+(3﹣3m)2=2,解得:m=![]() (不合题意值已舍去);
(不合题意值已舍去);
当AE=ED时,同理可得:m=![]() ;
;
综上,点E的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
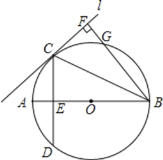
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
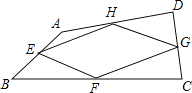
【题目】(满分8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是____________;
(2)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是( )
A. 随着抛掷次数的增加,正面朝上的频率越来越小
B. 当抛掷的次数很大时,正面朝上的次数一定占总抛掷次数的![]()
C. 不同次数的试验,正面朝上的频率可能会不相同
D. 连续抛掷11次硬币都是正面朝上,第12次抛掷出现正面朝上的概率小于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
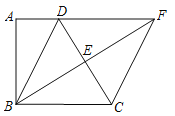
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
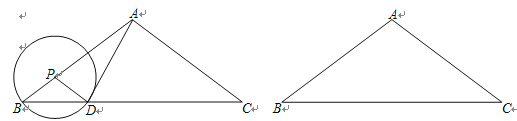
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①由4根火柴棍围成;图②由12根火柴棍围成;图③由24根火柴棍围成;…按此规律,则第⑥个图形由( )根火柴棍围成.
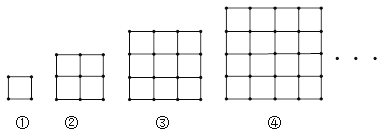
A. 60 B. 72 C. 84 D. 112
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com