
分析 首先化简x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=5+2$\sqrt{6}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=5-2$\sqrt{6}$,进一步利用完全平方公式整理代数式代入求得答案即可.
解答 解:∵x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=5+2$\sqrt{6}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=5-2$\sqrt{6}$,
∴x4+y4
=(x2+y2)2-2x2y2
=[(5+2$\sqrt{6}$)2+(5-2$\sqrt{6}$)2]2-2[(5+2$\sqrt{6}$)(5-2$\sqrt{6}$)]2
=(49+20$\sqrt{6}$+49-20$\sqrt{6}$)2-2
=982-2
=9602.
点评 此题考查二次根式的化简求值,掌握化简的方法以及完全平方公式是解决问题的关键.


科目:初中数学 来源: 题型:填空题
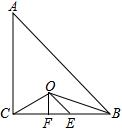 Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为8.
Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+(10-x)=14 | B. | 3x-(10-x)=14 | C. | 3x+x=14 | D. | 3x-x=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com