
分析 (1)由题意可知:A种型号衣服10件×进价+B种型号衣服8件×进价=1700,A种型号衣服9件×进价+B种型号衣服10件×进价=1810;由此列出方程组解答即可;
(2)根据获利不少于798元,且A型号衣服不多于28件,列出不等式组解答即可.
解答 解:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则:$\left\{\begin{array}{l}{10x+8y=1700}\\{9x+10y=1810}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=90}\\{y=100}\end{array}\right.$.
答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得:$\left\{\begin{array}{l}{18(2m+4)+30m≥798}\\{2m+4≤28}\end{array}\right.$
解得11≤m≤12,
∵m为正整数,
∴m=11、12,2m+4=26、28.
有两种进货方案:
(1)B型号衣服购买11件,A型号衣服购进26件;
(2)B型号衣服购买12件,A型号衣服购进28件.
点评 此题考查二元一次方程组与一元一次不等式组的实际运用,解决本题的关键是读懂题意,找到符合题意的不等关系与等量关系.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
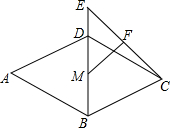 已知:如图,菱形ABCD的边长为4,∠A=60°,M是对角线BD的中点,延长BD到点E,连接EC,F是EC的中点
已知:如图,菱形ABCD的边长为4,∠A=60°,M是对角线BD的中点,延长BD到点E,连接EC,F是EC的中点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
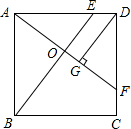 如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
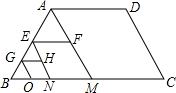 如图,四边形ABCD是等腰梯形,BC=2AD=4,过A作AM∥DC,得到第1个三角形,其平行于BC的中位线EF=1;过E作EN∥DC,得到第2个三角形,其平行于BC的中位线GH=$\frac{1}{2}$;过G作GO∥DC,得到第3个三角形,….按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$.(用正整数n表示)
如图,四边形ABCD是等腰梯形,BC=2AD=4,过A作AM∥DC,得到第1个三角形,其平行于BC的中位线EF=1;过E作EN∥DC,得到第2个三角形,其平行于BC的中位线GH=$\frac{1}{2}$;过G作GO∥DC,得到第3个三角形,….按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$.(用正整数n表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3 | B. | a≤3 | C. | a>3 | D. | a≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
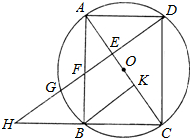 如图,已知:矩形ABCD,以对角线AC的中点O为圆心,OA的长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为点K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
如图,已知:矩形ABCD,以对角线AC的中点O为圆心,OA的长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为点K,过点D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
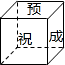 李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )
李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )| A. | 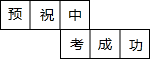 | B. | 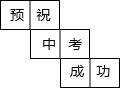 | C. | 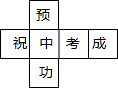 | D. | 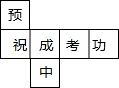 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com