
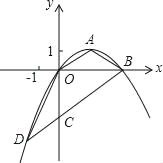
【题目】如图,顶点为A(![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x;(2)见解析;(3)点P的坐标为(﹣
x;(2)见解析;(3)点P的坐标为(﹣![]() ,0)
,0)
【解析】试题分析:(1)用待定系数法求出抛物线解析式,(2)先求出直线OA对应的一次函数的表达式为y=![]() x.再求出直线BD的表达式为y=
x.再求出直线BD的表达式为y=![]() x﹣2.最后求出交点坐标C,D即可;
x﹣2.最后求出交点坐标C,D即可;
(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
试题解析:解:(1)∵抛物线顶点为A(![]() ,1),设抛物线解析式为y=a(x﹣
,1),设抛物线解析式为y=a(x﹣![]() )2+1,将原点坐标(0,0)在抛物线上,∴0=a(
)2+1,将原点坐标(0,0)在抛物线上,∴0=a(![]() )2+1
)2+1
∴a=﹣![]() ,∴抛物线的表达式为:y=﹣
,∴抛物线的表达式为:y=﹣![]() x2+
x2+![]() x.
x.
(2)令y=0,得 0=﹣![]() x2+
x2+![]() x,∴x=0(舍),或x=2
x,∴x=0(舍),或x=2![]()
∴B点坐标为:(2![]() ,0),设直线OA的表达式为y=kx.∵A(
,0),设直线OA的表达式为y=kx.∵A(![]() ,1)在直线OA上,∴
,1)在直线OA上,∴![]() k=1,∴k=
k=1,∴k=![]() ,∴直线OA对应的一次函数的表达式为y=
,∴直线OA对应的一次函数的表达式为y=![]() x.
x.
∵BD∥AO,设直线BD对应的一次函数的表达式为y=![]() x+b.∵B(2
x+b.∵B(2![]() ,0)在直线BD上,∴0=
,0)在直线BD上,∴0=![]() ×2
×2![]() +b,∴b=﹣2,∴直线BD的表达式为y=
+b,∴b=﹣2,∴直线BD的表达式为y=![]() x﹣2.
x﹣2.

由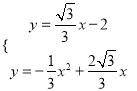
得交点D的坐标为(﹣![]() ,﹣3),令x=0得,y=﹣2,∴C点的坐标为(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2
,﹣3),令x=0得,y=﹣2,∴C点的坐标为(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2![]() =OD.
=OD.
在△OAB与△OCD中,  ,∴△OAB≌△OCD.
,∴△OAB≌△OCD.
(3)点C关于x轴的对称点C'的坐标为(0,2),∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,∴PO∥DQ,∴△C'PO∽△C'DQ,∴![]() ,∴
,∴![]() ,∴PO=
,∴PO=![]() ,∴点P的坐标为(﹣
,∴点P的坐标为(﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
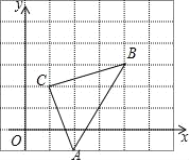
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ 、 )
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列不等式组解应用题:我校新校区![]() 级新生中有女生若干名需住校,已知我校新校区有若干间宿舍,每间住
级新生中有女生若干名需住校,已知我校新校区有若干间宿舍,每间住![]() 人,剩
人,剩![]() 人无房住;每间住
人无房住;每间住![]() 人,有一间宿舍住不满,问可能有多少间宿舍,多少名女生?
人,有一间宿舍住不满,问可能有多少间宿舍,多少名女生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,AB=3,BC=4.将△BCD沿对角线BD翻折得到△BED,BE交AD于点O.
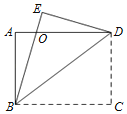
(1)判断△BOD的形状,并证明;(2)直接写出线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2018年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生![]() 已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com