
ШчЭМЃЌСНИіБпГЄОљЮЊ2ЕФе§ЗНаЮABCDКЭе§ЗНаЮCDEFЃЌЕуBЁЂCЁЂFдкЭЌвЛжБЯпЩЯЃЌвЛжБНЧШ§НЧАхЕФжБНЧЖЅЕуЗХжУдкDЕуДІЃЌDPНЛABгкЕуMЃЌDQНЛBFгкЕуNЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїDBMЁеЁїDFNЃЛЃЈ4ЗжЃЉ
ЃЈ2ЃЉбгГЄе§ЗНаЮЕФБпCBКЭEFЃЌЗжБ№гыжБНЧШ§НЧАхЕФСНБпDPЁЂDQЃЈЛђЫќУЧЕФбгГЄЯпЃЉНЛгкЕуGКЭЕуHЃЌЪдЬНОПЯТСаЮЪЬтЃК
ЂйЯпЖЮBGгыFHЯрЕШТ№ЃПЫЕУїРэгЩЃЛЃЈ4ЗжЃЉ
ЂкЕБЯпЖЮFNЕФГЄЪЧЗНГЬ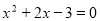 ЕФвЛИљЪБЃЌЪдЧѓГі
ЕФвЛИљЪБЃЌЪдЧѓГі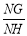 ЕФжЕЃЎЃЈ4ЗжЃЉ
ЕФжЕЃЎЃЈ4ЗжЃЉ

ЃЈ1ЃЉжЄУїМћНтЮіЃЛ
ЃЈ2ЃЉЂйBG=FHЃЎРэгЩМћНтЮіЃЛ
Ђк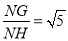 ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉШчЭМ1ЃЌИљОне§ЗНаЮЕФаджЪОЭПЩЕУГіBD=FDЃЌЁЯADB=ЁЯCDF=ЁЯADB=ЁЯCFD=45ЁуЃЌгЩжБНЧШ§НЧаЮЕФаджЪОЭПЩвдЕУГіЁЯ1=ЁЯADMЃЌНјЖјЕУГіЁЯ3=ЁЯ4ЃЌгЩASAОЭПЩвдЕУГіНсТлЃЛ
ЃЈ2ЃЉЂйШчЭМ1ЃЌИљОне§ЗНаЮЕФаджЪМАжБНЧШ§НЧаЮЕФаджЪОЭПЩвдЕУГіЁїGCDЁеЁїHEDОЭгаCG=EHЃЌгЩЕШЪНЕФаджЪОЭПЩвдЕУГіНсТлЃЛ
ЂкЯШНтЗНГЬx2+2xЉ3=0ОЭПЩвдЧѓГіFN=1ЃЌЕУГіCN=1ЃЌШчЭМ2ЃЌОЭПЩвдЕУГіЁїCNDЁеЁїFNHЃЌЕУГіCD=FH=2ЃЌОЭПЩвдЕУГіGB=2ЃЌGN=5ЃЌгЩЙДЙЩЖЈРэОЭПЩвдЧѓГіNHЕФжЕЃЌНјЖјЕУГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1ЃЌ
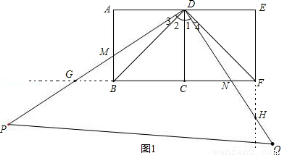
ЁпЫФБпаЮABCDКЭЫФБпаЮCDEFЪЧе§ЗНаЮЃЌ
ЁрBC=FCЃЌBD=FDЃЌЁЯABD=ЁЯADB=ЁЯCDF=ЁЯADB=ЁЯCFD=45ЁуЃЌЁЯDCB=ЁЯDEF=ЁЯE=ЁЯHFN=ЁЯADC=90ЁуЃЎ
ЁрЁЯADM+ЁЯCDM=90ЁуЃЌ
ЁпЁЯPDQ=90ЁуЃЌ
ЁрЁЯCDM+ЁЯCDN=90ЁуЃЎ
ЁрЁЯADM=ЁЯCDNЃЎ
ЁрЁЯADBЉЁЯADM=ЁЯCDFЉЁЯCDNЃЌ
ЁрЁЯMDB=ЁЯNDFЃЎ
дкЁїDBMКЭЁїDFNжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїDBMЁеЁїDFNЃЈASAЃЉЃЛ
ЃЈ2ЃЉЂйЫФБпаЮABCDКЭЫФБпаЮCDEFЪЧе§ЗНаЮЃЌ
ЁрBC=FC=EFЃЌBD=FDЃЌЁЯABD=ЁЯADB=ЁЯCDF=ЁЯADB=ЁЯCFD=45ЁуЃЌЁЯDCB=ЁЯDEF=ЁЯCDE=ЁЯE=ЁЯHFN=ЁЯADC=90ЁуЃЎ
ЁрЁЯEDH+ЁЯ1=90ЁуЃЌ
ЁпЁЯPDQ=90ЁуЃЌ
ЁрЁЯCDM+ЁЯ1=90ЁуЃЎ
ЁрЁЯCDM=ЁЯEDHЃЎ
дкЁїCDGКЭЁїEDHжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїCDGЁеЁїEDHЃЈASAЃЉЃЌ
ЁрCG=EHЃЌ
ЁрCGЉCB=EHЉEFЃЌ
ЁрBG=FHЃЎ
ЂкЁпx2+2xЉ3=0ЃЌ
Ёрx1=1ЃЌx2=Љ3ЃЎ
ЁпFNЕФГЄЪЧЗНГЬx2+2xЉ3=0ЕФвЛИљЃЌ
ЁрFN=1ЃЎ
ЁрCN=1ЃЌ
ЁрCN=FNЃЎ
ШчЭМ2ЃЌ
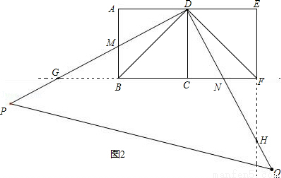
дкЁїCNDКЭЁїFNHжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїCNDЁеЁїFNHЃЈASAЃЉЃЌ
ЁрCD=FH=2ЃЌ
ЁрGB=2ЃЌ
ЁрGN=5ЃЎ
дкRtЁїFNHжаЃЌгЩЙДЙЩЖЈРэЃЌЕУNH=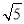 ЃЎ
ЃЎ
Ёр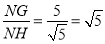 ЃЎ
ЃЎ
ПМЕуЃКЫФБпаЮзлКЯЬтЃЎ


 ФЯДѓНЬИЈЧРЯШЦ№ХмЪюМйЯЮНгНЬГЬФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
ФЯДѓНЬИЈЧРЯШЦ№ХмЪюМйЯЮНгНЬГЬФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁАЫФъМЖЯТбЇЦкЦкжаСЊПМЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
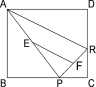
ШчгвЩЯЭМЃЌвбжЊОиаЮABCDжаЃЌPЁЂRЗжБ№ЪЧBCЁЂDCЩЯЕФЕуЃЌEЁЂFЗжБ№ЕФЪЧPAЁЂPRЕФжаЕуЃЌШчЙћDR=3ЃЌAD = 4ЃЌдђEFГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁЫежнЪаЯрГЧЧјАЫФъМЖЯТбЇЦкЦкФЉПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ОиаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЁЯAODЃН120ЁуЃЌACЃН8ЃЌдђЁїABOЕФжмГЄЮЊЃЈ ЃЉ
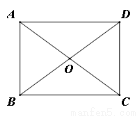
AЃЎ12 BЃЎ16 CЃЎ20 DЃЎ24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁбЮГЧЪаЖЋЬЈЪаАЫФъМЖЯТбЇЦкЕквЛДЮдТПМЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
вбжЊЁѕABCDЕФЖдНЧЯпЯрНЛгкЕуOЃЌШчЙћЁїAOBЕФУцЛ§ЪЧ3ЃЌФЧУДЁѕABCDЕФУцЛ§ЕШгк_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁбЮГЧЪаЖЋЬЈЪаАЫФъМЖЯТбЇЦкЕквЛДЮдТПМЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ЯТСаЪТМўЪЧБиШЛЗЂЩњЪТМўЕФЪЧЃЈЁЁЁЁЃЉ
AЃЎДђПЊЕчЪгЛњЃЌе§дкзЊВЅзуЧђБШШќ
BЃЎаЁТѓЕФФЖВњСПвЛЖЈЮЊ1500ЧЇПЫ
CЃЎдкжЛзАга5ИіКьЧђЕФДќжаУўГі1ЧђЃЌЪЧКьЧђ
DЃЎХЉРњЪЎЮхЕФЭэЩЯвЛЖЈФмПДЕНдВдТ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁЬЉжнЪаНЊбпЧјАЫФъМЖЯТбЇЦкЦкФЉПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ШчЭМЃЌEЃЌFЪЧЫФБпаЮABCDЖдНЧЯпACЩЯЕФСНЕуЃЌADЁЮBC ЃЌDFЁЮBE ЃЌAEЃНCFЃЎ
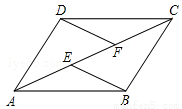
ЧѓжЄЃКЃЈ1ЃЉЁїAFDЁеЁїCEBЃЛЃЈ4ЗжЃЉ
ЃЈ2ЃЉЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЎЃЈ4ЗжЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁЬЉжнЪаНЊбпЧјАЫФъМЖЯТбЇЦкЦкФЉПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШєЙигк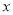 ЕФЗжЪНЗНГЬ
ЕФЗжЪНЗНГЬ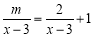 гадіИљЃЌдђ
гадіИљЃЌдђ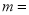 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁНвѕЪаАЫФъМЖЯТбЇЦкЦкжаПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
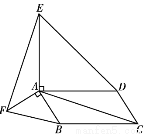
ШчЭМЃЌдкЁѕABCDЕФаЮЭтЗжБ№зїЕШбќжБНЧЁїABFКЭЕШбќжБНЧЁїADEЃЌЁЯFAB=ЁЯEAD=90ЁуЃЌ
СЌНсACЁЂEFЃЎдкЭМжаеввЛИігыЁїFAEШЋЕШЕФШ§НЧаЮЃЌВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2015НьНЫеЪЁаФаЃШ§аЃАЫФъМЖЯТбЇЦкЕкШ§ДЮСЊПМЪ§бЇОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
Шєга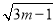 втвхЃЌдђmФмШЁЕФзюаЁећЪ§жЕЪЧЃЈ ЃЉ
втвхЃЌдђmФмШЁЕФзюаЁећЪ§жЕЪЧЃЈ ЃЉ
AЃЎm=0 BЃЎm=1 CЃЎm=2 DЃЎm=3
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com