
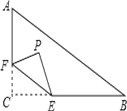
【题目】如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点E从C点出发向终点B运动,速度为1cm/秒,运动时间为t秒,作EF∥AB,点P是点C关于FE的对称点,连接AP,当△AFP恰好是直角三角形时,t的值为______
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
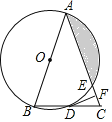
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( ).
①OG=![]() AB;
AB;
②与△EGD全等的三角形共有5个;
③S四边形ODGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
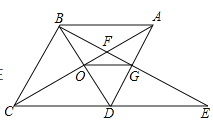
A.①③④B.①④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个抛物线形状与二次函数y=x2的图象形状和顶点相同,但开口方向不同.
(1)求抛物线解析式.
(2)如果该抛物线与一次函数y=kx﹣2相交于A、B两点,已知A点的纵坐标为﹣1,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是ΔABC的边BC的中点,AN平分![]() BAC, BN
BAC, BN![]() AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
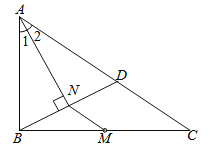
(1)求证:ΔBAN≌ΔDAN
(2)求ΔABC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:己知二次函数y=2x2﹣8x+6.
(1)用配方法将函数关系式化为y=a(x﹣h)2+k的形式,并写出函数的对称轴和顶点坐标;
(2)函数图象与x轴交于A、B两点,与y轴交于点C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与双曲线y=![]() 在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
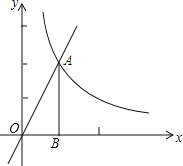
A.(2,0) B.(2,﹣1) C.(﹣2,1) D.(﹣1,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com