
【题目】如图,M是ΔABC的边BC的中点,AN平分![]() BAC, BN
BAC, BN![]() AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
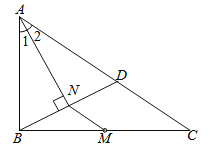
(1)求证:ΔBAN≌ΔDAN
(2)求ΔABC的周长
【答案】(1)详见解析;(2)41
【解析】
(1)根据题意∠1=∠2,AN=AN,∠ANB=∠AND=90°,即可证明ΔBAN≌ΔDAN;
(2)由(1)可知,AB=AD,N为BD的中点,则MN为中位线,得CD=2MN,然后计算可得周长.
解:(1)∵AN平分![]() BAC,
BAC,
∴∠1=∠2,
∵BN![]() AN,
AN,
∴∠ANB=∠AND=90°,
∵AN=AN,
∴ΔBAN≌ΔDAN(ASA);
(2)由ΔBAN≌ΔDAN,
∴AB=AD,BN=DN,
∴N为BD的中点,
∵M是ΔABC的边BC的中点,
∴MN为△BCD的中位线,
∴CD=2MN=6,
∵AB=AD=10,BC=15,
∴ΔABC的周长=AB+BC+AC=AB+BC+AD+DC=10+15+10+6=41.


科目:初中数学 来源: 题型:
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转![]() 得到正方形
得到正方形![]() 此时,点
此时,点![]() 落在对角线AC上,点
落在对角线AC上,点![]() 落在CD的延长线上
落在CD的延长线上![]() ,
,![]() 交AD于点E,连接
交AD于点E,连接![]() 、CE.
、CE.

求证:(1)![]() ≌
≌![]() ;
;
(2)直线CE是线段![]() 的垂直平分线.
的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB,PE与DC交于点O.
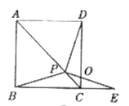
(基础探究)
(1)求证:PD=PE.
(2)求证:∠DPE=90°
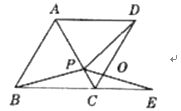
(3)(应用拓展)把正方形ABCD改为菱形,其他条件不变(如图),若PE=3,则PD=________;
若∠ABC=62°,则∠DPE=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°,连接OD,则OD长的最大值为 ( )
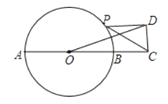
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
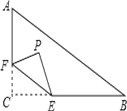
【题目】如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,点E从C点出发向终点B运动,速度为1cm/秒,运动时间为t秒,作EF∥AB,点P是点C关于FE的对称点,连接AP,当△AFP恰好是直角三角形时,t的值为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种水果,迸价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种牛奶的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
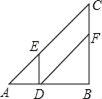
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,
求:出发几秒时,四边形DFCE的面积为20cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
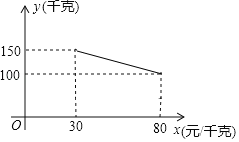
【题目】某超市销售一种商品,成本价为20元/千克,经市场调查,每天销售量y(千克)与销售单价x(元千克)之间的关系如图所示,规定每千克售价不能低于30元,且不高于80元.
(1)直接写出y与x之间的函数关系式;
(2)如果该超市销售这种商品每天获得3900元的利润,那么该商品的销售单价为多少元?
(3)设每天的总利润为w元,当销售单价定为多少元时,该超市每天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com