
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转![]() 得到正方形
得到正方形![]() 此时,点
此时,点![]() 落在对角线AC上,点
落在对角线AC上,点![]() 落在CD的延长线上
落在CD的延长线上![]() ,
,![]() 交AD于点E,连接
交AD于点E,连接![]() 、CE.
、CE.

求证:(1)![]() ≌
≌![]() ;
;
(2)直线CE是线段![]() 的垂直平分线.
的垂直平分线.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若小明将一袋分好类的生活垃圾随机投入一类垃圾箱,请画树状图或列表求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共100吨生活垃圾,数据统计如下表(单位:吨):
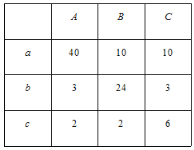
试估计该小区居民“厨余垃圾”投放正确的概率约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣4x﹣5经过点A(﹣1,0)、B(5,0)
(1)当0<x<5时,y的取值范围为 ;
(2)点P为抛物线上一点,若△PAB的面积S△PAB=21,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原来公园有一个半径为 1 m 的苗圃,现在准备扩大面积,设当扩大后的半径为x m时,则增加的环形的面积为y m 2 .
(1)写出y与x的函数关系式;
(2)当半径增大到多少时面积增大1倍;
(3)试猜测半径是多少时,面积是原来的3、4、5、…倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
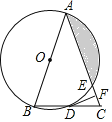
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).
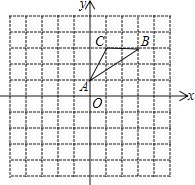
(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
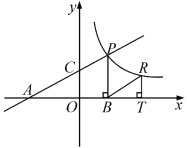
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),直线
的左侧),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ..
..
(1)求抛物线与x轴的交点坐标;
(2)设点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是ΔABC的边BC的中点,AN平分![]() BAC, BN
BAC, BN![]() AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
AN于点N延长BN交AC于点D,已知AB=10,BC=15,MN=3
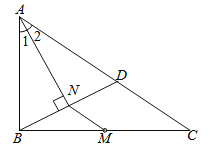
(1)求证:ΔBAN≌ΔDAN
(2)求ΔABC的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com