
����Ŀ��С��Ϊ�˴ٽ����������ķ��ദ����������������Ϊ���ࡢ�ɻ��պ��������࣬�ֱ��Ϊa��b��c��������������Ӧ�������䣬�������������䡢���ɻ������͡������������䣬�ֱ��ΪA��B��C��
��1����С����һ���ֺ���������������Ͷ��һ�������䣬�뻭��״ͼ���б�������Ͷ����ȷ�ĸ��ʣ�
��2��Ϊ�������������������Ͷ��������������ȡ�˸�С���������������ܹ�100����������������ͳ�����±�����λ���֣���
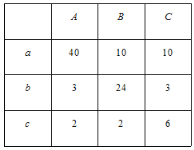
�Թ��Ƹ�С��������������Ͷ����ȷ�ĸ���Լ�Ƕ��٣�
���𰸡���1��P������Ͷ����ȷ����![]() ����2�����Ƹ�С��������������Ͷ����ȷ�ĸ���ԼΪ
����2�����Ƹ�С��������������Ͷ����ȷ�ĸ���ԼΪ![]() ��
��
��������
��1�����Ȼ�����״ͼ������״ͼ��֪����Ϊ9��Ͷ����ȷ����3�֣������������Ͷ����ȷ�Ĺ��ɣ�
��2�����������Լ����ʵĶ���������ɼ��ɡ�
��1����ͼ��ʾ��
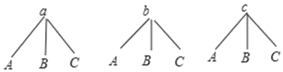
С����һ���ֺ���������������Ͷ��һ�������䣻����9�������
����Ͷ����ȷ����3�������
��P������Ͷ����ȷ����![]() ��
��![]() ��
��
��2����![]() ��
��
����Ƹ�С��������������Ͷ����ȷ�ĸ���ԼΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
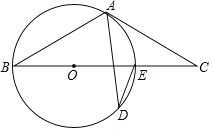
����Ŀ����ͼ��BE��O��ֱ������A�͵�D�ǡ�O�ϵ����㣬����A����O�����߽�BE�ӳ����ڵ㣮
��1������ADE=25�������C�Ķ�����
��2����AB=AC��CE=2�����O�뾶�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����x�������A.B���㣬��y���ཻ�ڵ�C��0��-3���������ߵĶԳ���Ϊֱ��x=1.
��ͼ����x�������A.B���㣬��y���ཻ�ڵ�C��0��-3���������ߵĶԳ���Ϊֱ��x=1.

��1������κ����Ľ���ʽ��
��2���������ߵĶ���ΪD����E���������ϣ������C���������ߵĶԳ���Գƣ�ֱ��AE���Գ����ڵ�F�����ж��ı���CDEF����״����˵�����ɣ�
��3������M��x���ϣ���P���������ϣ��Ƿ�����Ե�A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ������ڣ��������������Ҫ��ĵ�P�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������O��AC�ϣ���OAΪ�뾶����O��AB�ڵ�D��BD�Ĵ�ֱƽ���߽�BC�ڵ�E����BD�ڵ�F������DE��
��1���ж�ֱ��DE����O��λ�ù�ϵ����˵�����ɣ�
��2����AC=6��BC=8��OA=2�����߶�DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
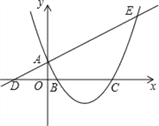
����Ŀ����ͼ����ֱ֪��y=![]() x+1��y�ύ�ڵ�A����x�ύ�ڵ�D��������y=
x+1��y�ύ�ڵ�A����x�ύ�ڵ�D��������y= ![]() x2+bx+c��ֱ�߽���A��E���㣬��x�ύ��B��C���㣬��B������Ϊ��1��0�����������ߵĶԳ�������һ��M��ʹ|AM��MC|��ֵ��������M������__________.
x2+bx+c��ֱ�߽���A��E���㣬��x�ύ��B��C���㣬��B������Ϊ��1��0�����������ߵĶԳ�������һ��M��ʹ|AM��MC|��ֵ��������M������__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���![]()
��1����֤������mȡ��ֵʱ������������������ȵ�ʵ����
��2�������̵�һ����Ϊ1����m��ֵ�����̵���һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
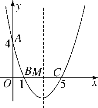
����Ŀ����ͼ,��ֱ������ϵ�У������߾�����A(0��4)��B(1��0)��C(5��0)����Գ�����x���ཻ�ڵ�M.
(1)�������ߵĽ���ʽ�ͶԳ��
(2)�������ߵĶԳ������Ƿ����һ��P��ʹ��PAB���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
(3)����AC����ֱ��AC���·����������ϣ��Ƿ����һ��N��ʹ��NAC�������������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���һ����λ���ȣ���
��1��������ABC����ƽ��4����λ���ȵõ�����A1B1C1����C1���������� ��
��2���Ե�BΪλ�����ģ��������ڻ�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1����C2���������� ����
��3����A2B2C2��������� ��ƽ����λ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��������ABCD�Ƶ�C��˳ʱ�뷽����ת![]() �õ�������
�õ�������![]() ��ʱ,��
��ʱ,��![]() ���ڶԽ���AC��,��
���ڶԽ���AC��,��![]() ����CD���ӳ�����
����CD���ӳ�����![]() ,
,![]() ��AD�ڵ�E,����
��AD�ڵ�E,����![]() ��CE��
��CE��

��֤��(1)![]() ��
��![]() ��
��
(2)ֱ��CE���߶�![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com